G-expectation
In probability theory, the g-expectation is a nonlinear expectation based on a backwards stochastic differential equation (BSDE) originally developed by Shige Peng.[1]
Definition
Given a probability space 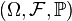 with
with 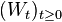 is a (d-dimensional) Wiener process (on that space). Given the filtration generated by
is a (d-dimensional) Wiener process (on that space). Given the filtration generated by  , i.e.
, i.e. ![\mathcal{F}_t = \sigma(W_s: s \in [0,t])](../I/m/739020a3a84139f8a5fb16a1e131482a.png) , let
, let 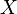 be
be 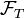 measurable. Consider the BSDE given by:
measurable. Consider the BSDE given by:
Then the g-expectation for 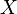 is given by
is given by ![\mathbb{E}^g[X] := Y_0](../I/m/b0432efb21f796bf68defe431a96b291.png) . Note that if
. Note that if 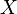 is an m-dimensional vector, then
is an m-dimensional vector, then 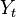 (for each time
(for each time 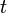 ) is an m-dimensional vector and
) is an m-dimensional vector and 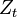 is an
is an 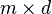 matrix.
matrix.
In fact the conditional expectation is given by ![\mathbb{E}^g[X \mid \mathcal{F}_t] := Y_t](../I/m/71a56ca189c4bfb007cce793207110fb.png) and much like the formal definition for conditional expectation it follows that
and much like the formal definition for conditional expectation it follows that ![\mathbb{E}^g[1_A \mathbb{E}^g[X \mid \mathcal{F}_t]] = \mathbb{E}^g[1_A X]](../I/m/6b2c750a5ecae31f5dfa7f562f71edbe.png) for any
for any 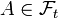 (and the
(and the 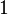 function is the indicator function).[1]
function is the indicator function).[1]
Existence and uniqueness
Let ![g: [0,T] \times \mathbb{R}^m \times \mathbb{R}^{m \times d} \to \mathbb{R}^m](../I/m/ce3c1c4d7105dc0d4b5787fd1cfba233.png) satisfy:
satisfy:
-
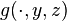 is an
is an 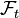 -adapted process for every
-adapted process for every 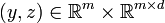
-
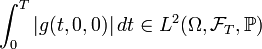 the L2 space (where
the L2 space (where  is a norm in
is a norm in 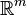 )
) -
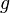 is Lipschitz continuous in
is Lipschitz continuous in 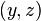 , i.e. for every
, i.e. for every 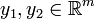 and
and 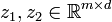 it follows that
it follows that 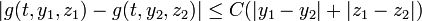 for some constant
for some constant 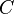
Then for any random variable 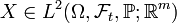 there exists a unique pair of
there exists a unique pair of 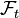 -adapted processes
-adapted processes 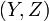 which satisfy the stochastic differential equation.[2]
which satisfy the stochastic differential equation.[2]
In particular, if 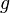 additionally satisfies:
additionally satisfies:
-
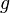 is continuous in time (
is continuous in time (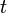 )
) -
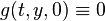 for all
for all ![(t,y) \in [0,T] \times \mathbb{R}^m](../I/m/f1507c38a5a5f714d9f7b23a2727ee15.png)
then for the terminal random variable 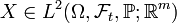 it follows that the solution processes
it follows that the solution processes 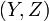 are square integrable. Therefore
are square integrable. Therefore ![\mathbb{E}^g[X | \mathcal{F}_t]](../I/m/8f1c6deed92c4940e32b2bbd342138d8.png) is square integrable for all times
is square integrable for all times 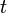 .[3]
.[3]
See also
- Expected value
- Choquet expectation
- Risk measure – almost any time consistent convex risk measure can be written as
![\rho_g(X) := \mathbb{E}^g[-X]](../I/m/88de2e920dc78f5cff263b217fa0fba4.png) [4]
[4]
References
- ↑ 1.0 1.1 Philippe Briand; François Coquet; Ying Hu; Jean Mémin; Shige Peng (2000). "A Converse Comparison Theorem for BSDEs and Related Properties of g-Expectation" (pdf). Electronic Communications in Probability 5 (13): 101–117. doi:10.1214/ecp.v5-1025. Retrieved August 2, 2012.
- ↑ Peng, S. (2004). "Nonlinear Expectations, Nonlinear Evaluations and Risk Measures". Stochastic Methods in Finance (pdf). Lecture Notes in Mathematics 1856. pp. 165–138. doi:10.1007/978-3-540-44644-6_4. ISBN 978-3-540-22953-7. Retrieved August 9, 2012.
- ↑ Chen, Z.; Chen, T.; Davison, M. (2005). "Choquet expectation and Peng's g -expectation". The Annals of Probability 33 (3): 1179. doi:10.1214/009117904000001053.
- ↑ Rosazza Gianin, E. (2006). "Risk measures via g-expectations". Insurance: Mathematics and Economics 39: 19–65. doi:10.1016/j.insmatheco.2006.01.002.