Gδ set
In the mathematical field of topology, a Gδ set is a subset of a topological space that is a countable intersection of open sets. The notation originated in Germany with G for Gebiet (German: area, or neighborhood) meaning open set in this case and δ for Durchschnitt (German: intersection). The term inner limiting set is also used. Gδ sets, and their dual Fσ sets, are the second level of the Borel hierarchy.
Definition
In a topological space a Gδ set is a countable intersection of open sets. The Gδ sets are exactly the level 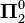 sets of the Borel hierarchy.
sets of the Borel hierarchy.
Examples
- Any open set is trivially a Gδ set
- The irrational numbers are a Gδ set in the real numbers R. They can be written as the countable intersection of the sets {q}C where q is rational.
- The set of rational numbers Q is not a Gδ set in R. If Q were the intersection of open sets An, each An would be dense in R because Q is dense in R. However, the construction above gave the irrational numbers as a countable intersection of open dense subsets. Taking the intersection of both of these sets gives the empty set as a countable intersection of open dense sets in R, a violation of the Baire category theorem.
- The zero-set of a derivative of an everywhere differentiable real-valued function on R is a Gδ set; it can be a dense set with empty interior, as shown by Pompeiu's construction.
A more elaborate example of a Gδ set is given by the following theorem:
Theorem: The set ![D=\left\{f \in C([0,1]) : f \text{ is not differentiable at any point of } [0,1] \right\}](../I/m/7b75287f137258a9478197c5cee60b1d.png) contains a dense Gδ subset of the metric space
contains a dense Gδ subset of the metric space ![C([0,1])](../I/m/8dbbcbb0e878bab88516ad2b7d27f8e0.png) . (See Weierstrass function#Density of nowhere-differentiable functions.)
. (See Weierstrass function#Density of nowhere-differentiable functions.)
Properties
The notion of Gδ sets in metric (and topological) spaces is strongly related to the notion of completeness of the metric space as well as to the Baire category theorem. This is described by the Mazurkiewicz theorem:
Theorem (Mazurkiewicz): Let 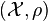 be a complete metric space and
be a complete metric space and 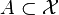 . Then the following are equivalent:
. Then the following are equivalent:
-
 is a Gδ subset of
is a Gδ subset of 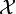
- There is a metric
 on
on  which is equivalent to
which is equivalent to 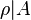 such that
such that 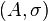 is a complete metric space.
is a complete metric space.
A key property of 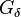 sets is that they are the possible sets at which a function from a topological space to a metric space is continuous. Formally: The set of points where a function
sets is that they are the possible sets at which a function from a topological space to a metric space is continuous. Formally: The set of points where a function  is continuous is a
is continuous is a 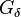 set. This is because continuity at a point
set. This is because continuity at a point  can be defined by a
can be defined by a 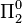 formula, namely: For all positive integers
formula, namely: For all positive integers  , there is an open set
, there is an open set  containing
containing  such that
such that 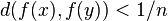 for all
for all 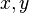 in
in  . If a value of
. If a value of  is fixed, the set of
is fixed, the set of  for which there is such a corresponding open
for which there is such a corresponding open  is itself an open set (being a union of open sets), and the universal quantifier on
is itself an open set (being a union of open sets), and the universal quantifier on  corresponds to the (countable) intersection of these sets. In the real line, the converse holds as well; for any Gδ subset A of the real line, there is a function f: R → R which is continuous exactly at the points in A. As a consequence, while it is possible for the irrationals to be the set of continuity points of a function (see the popcorn function), it is impossible to construct a function which is continuous only on the rational numbers.
corresponds to the (countable) intersection of these sets. In the real line, the converse holds as well; for any Gδ subset A of the real line, there is a function f: R → R which is continuous exactly at the points in A. As a consequence, while it is possible for the irrationals to be the set of continuity points of a function (see the popcorn function), it is impossible to construct a function which is continuous only on the rational numbers.
Basic properties
- The complement of a Gδ set is an Fσ set.
- The intersection of countably many Gδ sets is a Gδ set, and the union of finitely many Gδ sets is a Gδ set; a countable union of Gδ sets is called a Gδσ set.
- In metrizable spaces, every closed set is a Gδ set and, dually, every open set is an Fσ set.
- A subspace A of a completely metrizable space X is itself completely metrizable if and only if A is a Gδ set in X.
- A set that contains the intersection of a countable collection of dense open sets is called comeagre or residual. These sets are used to define generic properties of topological spaces of functions.
The following results regard Polish spaces:[1]
- Let
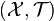 be a Polish topological space and let
be a Polish topological space and let 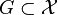 be a Gδ set (with respect to
be a Gδ set (with respect to 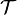 ). Then
). Then  is a Polish space with respect to the subspace topology on it.
is a Polish space with respect to the subspace topology on it.
- Topological characterization of Polish spaces: If
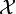 is a Polish space then it is homeomorphic to a Gδ subset of a compact metric space.
is a Polish space then it is homeomorphic to a Gδ subset of a compact metric space.
Gδ space
A Gδ space is a topological space in which every closed set is a Gδ set (Johnson 1970). A normal space which is also a Gδ space is perfectly normal. Every metrizable space is perfectly normal, and every perfectly normal space is completely normal: neither implication is reversible.
See also
- Fσ set, the dual concept; note that "G" is German (Gebiet) and "F" is French (fermé).
- P-space, any space having the property that every Gδ set is open
References
- Kelley, John L. (1955). General topology. van Nostrand. p. 134.
- Steen, Lynn Arthur; Seebach, J. Arthur Jr. (1995) [1978]. Counterexamples in Topology (Dover reprint of 1978 ed.). Berlin, New York: Springer-Verlag. ISBN 978-0-486-68735-3. MR 507446 P. 162.
- Fremlin, D.H. (2003) [2003]. "4, General Topology". Measure Theory, Volume 4. Petersburg, England: Digital Books Logostics. ISBN 0-9538129-4-4. Retrieved 1 April 2011 P. 334.
- Johnson, Roy A. (1970). "A Compact Non-Metrizable Space Such That Every Closed Subset is a G-Delta". The American Mathematical Monthly 77 (2): 172–176. JSTOR 2317335.
Notes
- ↑ Fremlin, D.H. (2003). "4, General Topology". Measure Theory, Volume 4. Petersburg, England: Digital Books Logistics. pp. 334–335. ISBN 0-9538129-4-4. Retrieved 1 April 2011.