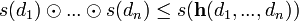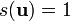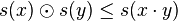Fuzzy subalgebra

Fuzzy subalgebras theory is a chapter of fuzzy set theory. It is obtained from an interpretation in a multi-valued logic of axioms usually expressing the notion of subalgebra of a given algebraic structure.

Definition

Consider a first order language for algebraic structures with a monadic predicate symbol S. Then a fuzzy subalgebra is a fuzzy model of a theory containing, for any n-ary operation h, the axioms

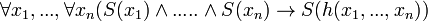
$\forall x_1, ..., \forall x_n (S(x_1) \and ..... \and S(x_n) \rightarrow S(h(x_1, ..., x_n))$

and, for any constant c, S(c).

The first axiom expresses the closure of S with respect to the operation h, and the second expresses the fact that c is an element in S. As an example, assume that the valuation structure is defined in [0,1] and denote by 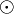$\odot$ the operation in [0,1] used to interpret the conjunction. Then a fuzzy subalgebra of an algebraic structure whose domain is D is defined by a fuzzy subset s : D → [0,1] of D such that, for every d₁,...,d_n in D, if h is the interpretation of the n-ary operation symbol h, then

$s(d_1) \odot... \odot s(d_n) \leq s(\bold{h}(d_1,...,d_n))$

Moreover, if c is the interpretation of a constant c such that s(c) = 1.

A largely studied class of fuzzy subalgebras is the one in which the operation 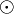$\odot$ coincides with the minimum. In such a case it is immediate to prove the following proposition.

Proposition. A fuzzy subset s of an algebraic structure defines a fuzzy subalgebra if and only if for every λ in [0,1], the closed cut {x ∈ D : s(x)≥ λ} of s is a subalgebra.

Fuzzy subgroups and submonoids

The fuzzy subgroups and the fuzzy submonoids are particularly interesting classes of fuzzy subalgebras. In such a case a fuzzy subset s of a monoid (M,•,u) is a fuzzy submonoid if and only if

$s(\bold{u})=1$
$s(x) \odot s(y) \leq s(x \cdot y)$

where u is the neutral element in A.

Given a group G, a fuzzy subgroup of G is a fuzzy submonoid s of G such that

s(x) ≤ s(x⁻¹).

It is possible to prove that the notion of fuzzy subgroup is strictly related with the notions of fuzzy equivalence. In fact, assume that S is a set, G a group of transformations in S and (G,s) a fuzzy subgroup of G. Then, by setting

e(x,y) = Sup{s(h) : h is an element in G such that h(x) = y}

we obtain a fuzzy equivalence. Conversely, let e be a fuzzy equivalence in S and, for every transformation h of S, set

s(h)= Inf{e(x,h(x)): x∈S}.

Then s defines a fuzzy subgroup of transformation in S. In a similar way we can relate the fuzzy submonoids with the fuzzy orders.

Bibliography

Klir, G. and Bo Yuan, Fuzzy Sets and Fuzzy Logic (1995) ISBN 978-0-13-101171-7
Zimmermann H., Fuzzy Set Theory and its Applications (2001), ISBN 978-0-7923-7435-0.
Chakraborty H. and Das S., On fuzzy equivalence 1, Fuzzy Sets and Systems, 11 (1983), 185-193.
Demirci M., Recasens J., Fuzzy groups, fuzzy functions and fuzzy equivalence relations, Fuzzy Sets and Systems, 144 (2004), 441-458.
Di Nola A., Gerla G., Lattice valued algebras, Stochastica, 11 (1987), 137-150.
Hájek P., Metamathematics of fuzzy logic. Kluwer 1998.
Klir G., UTE H. St.Clair and Bo Yuan Fuzzy Set Theory Foundations and Applications,1997.
Gerla G., Scarpati M., Similarities, Fuzzy Groups: a Galois Connection, J. Math. Anal. Appl., 292 (2004), 33-48.
Mordeson J., Kiran R. Bhutani and Azriel Rosenfeld. Fuzzy Group Theory, Springer Series: Studies in Fuzziness and Soft Computing, Vol. 182, 2005.
Rosenfeld A., Fuzzy groups, J. Math. Anal. Appl., 35 (1971), 512-517.
Zadeh L.A., Fuzzy Sets, ‘’Information and Control’’, 8 (1965) 338353.
Zadeh L.A., Similarity relations and fuzzy ordering, Inform. Sci. 3 (1971) 177–200.