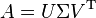Fundamental theorem of linear algebra
In mathematics, the fundamental theorem of linear algebra makes several statements regarding vector spaces. These may be stated concretely in terms of the rank r of an m × n matrix A and its singular value decomposition:
First, each matrix 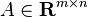 (
( has
has  rows and
rows and  columns) induces four fundamental subspaces. These fundamental subspaces are:
columns) induces four fundamental subspaces. These fundamental subspaces are:
| name of subspace | definition | containing space | dimension | basis |
|---|---|---|---|---|
| column space, range or image | 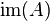 or or 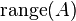 |
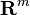 |
 (rank) (rank) |
The first  columns of columns of  |
| nullspace or kernel | 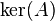 or or 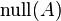 |
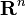 |
 (nullity) (nullity) |
The last 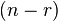 columns of columns of  |
| row space or coimage | 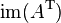 or or 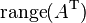 |
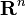 |
 (rank) (rank) |
The first  columns of columns of  |
| left nullspace or cokernel | 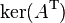 or or  |
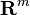 |
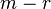 (corank) (corank) |
The last 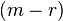 columns of columns of  |
Secondly:
- In
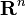 ,
, 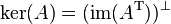 , that is, the nullspace is the orthogonal complement of the row space
, that is, the nullspace is the orthogonal complement of the row space - In
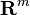 ,
, 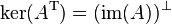 , that is, the left nullspace is the orthogonal complement of the column space.
, that is, the left nullspace is the orthogonal complement of the column space.

The four subspaces associated to a matrix A.
The dimensions of the subspaces are related by the rank–nullity theorem, and follow from the above theorem.
Further, all these spaces are intrinsically defined – they do not require a choice of basis – in which case one rewrites this in terms of abstract vector spaces, operators, and the dual spaces as 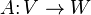 and
and 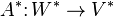 : the kernel and image of
: the kernel and image of 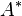 are the cokernel and coimage of
are the cokernel and coimage of  .
.
See also
References
- Strang, Gilbert. Linear Algebra and Its Applications. 3rd ed. Orlando: Saunders, 1988.
- Strang, Gilbert (1993), "The fundamental theorem of linear algebra", American Mathematical Monthly 100 (9): 848–855, doi:10.2307/2324660, JSTOR 2324660
External links
- Gilbert Strang, MIT Linear Algebra Lecture on the Four Fundamental Subspaces at Google Video, from MIT OpenCourseWare
| ||||||