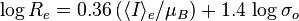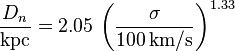Fundamental plane (elliptical galaxies)

For the concept in geometry, see Fundamental plane (spherical coordinates).

The fundamental plane is a set of bivariate correlations connecting some of the properties of normal elliptical galaxies, including their radius, luminosity, mass, velocity dispersion, metallicity, surface brightness, colors, density (of luminosity, mass, or phase space), and, to a lesser degree, the shape of their radial surface brightness profiles. It is usually expressed as a relationship between the effective radius, average surface brightness and central velocity dispersion of normal elliptical galaxies. Any one of the three parameters may be estimated from the other two, as together they describe a plane that falls within their more general three-dimensional space.

Motivation

Many characteristics of a galaxy are correlated. For example, as one would expect, a galaxy with a higher luminosity has a larger effective radius. The usefulness of these correlations is when a characteristic that can be determined without prior knowledge of the galaxy's distance (such as central velocity dispersion - the Doppler width of spectral lines in the central parts of the galaxy) can be correlated with a property, such as luminosity, that can be determined only for galaxies of a known distance. With this correlation, one can determine the distance to galaxies, a difficult task in astronomy.

Correlations

The following correlations have been empirically shown for elliptical galaxies:

Larger galaxies have fainter effective surface brightnesses. Mathematically speaking: 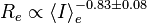$R_e \propto \langle I \rangle_e^{-0.83\pm0.08}$ (Djorgovski & Davis 1987),^[1] where 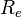$R_e$ is the effective radius, and 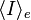$\langle I \rangle_e$ is the mean surface brightness interior to $R_e$ .
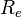As 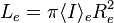$L_e = \pi \langle I \rangle_e R_e^2$ , we can substitute the previous correlation and see that 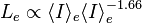$L_e \propto \langle I \rangle_e \langle I \rangle_e^{-1.66}$ and therefore: 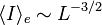$\langle I \rangle_e \sim L^{-3/2}$ meaning that more luminous ellipticals have lower surface brightnesses.
More luminous elliptical galaxies have larger central velocity dispersions. This is called the Faber–Jackson relation (Faber & Jackson 1976). Analytically this is: 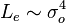$L_e \sim \sigma_o^4$ . This is analogous to the Tully–Fisher relation for spirals.
If central velocity dispersion is correlated to luminosity, and luminosity is correlated with effective radius, then it follows that the central velocity dispersion is positively correlated to the effective radius.

Usefulness

The usefulness of this three dimensional space 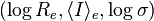$\left( \log R_e, \langle I \rangle_e, \log \sigma \right)$ is most practical when plotted as 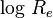$\log \, R_e$ against 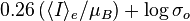$0.26 \, (\langle I \rangle_e/\mu_B) + \log \sigma_o$ . The equation of the regression line through this plot is:

\log R_e = 0.36 \,(\langle I \rangle_e / \mu_B) + 1.4 \, \log \sigma_o

Thus by measuring observable quantities such as surface brightness and velocity dispersion (both independent of the observer's distance to the source) one can estimate the effective radius (measured in kpc) of the galaxy. As one now knows the linear size of the effective radius and can measure the angular size, it is easy to determine the distance of the galaxy from the observer through the small-angle approximation.

Variations

An early use of the fundamental plane is the 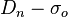$D_n - \sigma_o$ correlation, given by:

\frac{D_n}{\text{kpc}} = 2.05 \, \left(\frac{\sigma}{100 \, \text{km}/\text{s}}\right)^{1.33}

determined by Dressler et al. (1987). Here 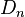$D_n$ is the diameter within which the mean surface brightness is 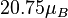$20.75 \mu_B$ . This relationship has a scatter of 15% between galaxies, as it represents a slightly oblique projection of the Fundamental Plane.

Fundamental Plane correlations provide insights into the formative and evolutionary processes of elliptical galaxies. Whereas the tilt of the Fundamental Plane relative to the naive expectations from the Virial Theorem is reasonably well understood, the outstanding puzzle is its small thickness.

Notes

Diffuse dwarf ellipticals do not lie on the fundamental plane as shown by Kormendy (1987). Gudehus (1991) found that galaxies brighter than 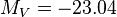$M_V=-23.04$ lie on one plane, and those fainter than this value, 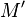$M '$ , lie on another plane. The two planes are inclined by about 11 degrees.

References

↑ Djorgovski, S., and Davis, M. "Fundamental properties of elliptical galaxies", Astrophys. J., vol. 313, pp. 50-69 (1987); downloadable through http://adsabs.harvard.edu/abs/1987ApJ...313...59D

Binney, J.; Merrifield, M. (1998). Galactic Astronomy. Princeton University Press. ISBN 0691004021.