Fundamental normality test

In complex analysis, a mathematical discipline, the fundamental normality test gives sufficient conditions to test the normality of a family of analytic functions.

Statement of theorem

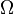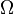Let $\mathcal{F}$ be a family of analytic functions defined on a domain $\Omega$ . If there are two fixed complex numbers a and b that are omitted from the range of every ƒ ∈ $\mathcal{F}$ , then $\mathcal{F}$ is a normal family on $\Omega$ .

The proof relies on properties of the elliptic modular function and can be found here: J. L. Schiff (1993). Normal Families. Springer-Verlag. ISBN 0-387-97967-0.

Fundamental normality test

Statement of theorem

See also