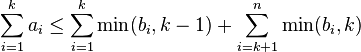Fulkerson–Chen–Anstee theorem
The Fulkerson–Chen–Anstee theorem is a result in graph theory, a branch of combinatorics. It provides one of two known approaches solving the digraph realization problem, i.e. it gives a necessary and sufficient condition for pairs of nonnegative integers 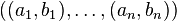 to be the indegree-outdegree pairs of a simple directed graph; a sequence obeying these conditions is called "digraphic". D. R. Fulkerson [1] (1960) obtained a characterization analogous to the classical Erdős–Gallai theorem for graphs, but in contrast to this solution with exponentially many inequalities. In 1966 Chen [2] improved this result in demanding the additional constraint that the integer pairs must be sorted in non-increasing lexicographical order leading to n inequalities. Anstee [3] (1982) observed in a different context that it is suffient to have
to be the indegree-outdegree pairs of a simple directed graph; a sequence obeying these conditions is called "digraphic". D. R. Fulkerson [1] (1960) obtained a characterization analogous to the classical Erdős–Gallai theorem for graphs, but in contrast to this solution with exponentially many inequalities. In 1966 Chen [2] improved this result in demanding the additional constraint that the integer pairs must be sorted in non-increasing lexicographical order leading to n inequalities. Anstee [3] (1982) observed in a different context that it is suffient to have 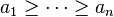 . Berger [4] reinvented this result and gives a direct proof.
. Berger [4] reinvented this result and gives a direct proof.
Theorem statement
A sequence 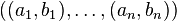 of nonnegative integer pairs with
of nonnegative integer pairs with 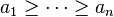 is digraphic if and only if
is digraphic if and only if 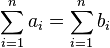 and the following inequality holds for k such that
and the following inequality holds for k such that 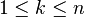 :
:
Stronger versions
Berger [4] proved that it suffices to consider the  th inequality such that
th inequality such that 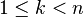 with
with 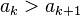 and for
and for 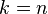 .
.
Other notations
The theorem can also be stated in terms of zero-one matrices. The connection can be seen if one realizes that each directed graph has an adjacency matrix where the column sums and row sums correspond to 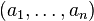 and
and  . Note that the diagonal of the matrix only contains zeros. There is a connection to the relation majorization. We define a sequence
. Note that the diagonal of the matrix only contains zeros. There is a connection to the relation majorization. We define a sequence 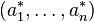 with
with 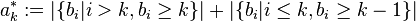 . Sequence
. Sequence 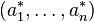 can also be determined by a corrected Ferrers diagram. Consider sequences
can also be determined by a corrected Ferrers diagram. Consider sequences 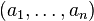 ,
,  and
and 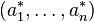 as
as  -dimensional vectors
-dimensional vectors  ,
,  and
and 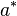 . Since
. Since 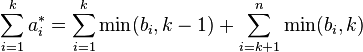 by applying the principle of double counting (proof technique), the theorem above states that a pair of nonnegative integer sequences
by applying the principle of double counting (proof technique), the theorem above states that a pair of nonnegative integer sequences 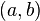 with nonincreasing
with nonincreasing  is digraphic if and only if vector
is digraphic if and only if vector 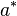 majorizes
majorizes  .
.
Generalization
A sequence 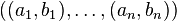 of nonnegative integer pairs with
of nonnegative integer pairs with 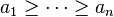 is digraphic if and only if
is digraphic if and only if 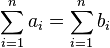 and there exists a sequence
and there exists a sequence  such that the pair
such that the pair 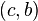 is digraphic and
is digraphic and  majorizes
majorizes  .[5]
.[5]
Characterizations for similar problems
Similar theorems describe the degree sequences of simple graphs, simple directed graphs with loops, and simple bipartite graphs. The first problem is characterized by the Erdős–Gallai theorem. The latter two cases, which are equivalent see Berger,[4] are characterized by the Gale–Ryser theorem.
See also
References
- ↑ D.R. Fulkerson: Zero-one matrices with zero trace. In: Pacific J. Math. No. 12, 1960, pp. 831–836
- ↑ Wai-Kai Chen: On the realization of a (p,s)-digraph with prescribed degrees . In: Journal of the Franklin Institute No. 6, 1966, pp. 406–422
- ↑ Richard Anstee: Properties of a class of (0,1)-matrices covering a given matrix. In: Can. J. Math., 1982, pp. 438–453
- ↑ 4.0 4.1 4.2 Annabell Berger: A Note on the Characterization of Digraphic Sequences In: Discrete Mathematics, 2014, pp. 38–41
- ↑ Annabell Berger: The connection between the number of realizations for degree sequences and majorization In: arXiv1212.5443, 2012