Fritz John conditions
The Fritz John conditions (abbr. FJ conditions), in mathematics, are a necessary condition for a solution in nonlinear programming to be optimal. They are used as lemma in the proof of the Karush–Kuhn–Tucker conditions, but they are relevant on their own.
We consider the following optimization problem:
where ƒ is the function to be minimized, 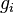 the inequality constraints and
the inequality constraints and 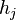 the equality constraints, and where, respectively,
the equality constraints, and where, respectively, 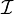 ,
, 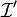 and
and 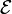 are the indices set of inactive, active and equality constraints and
are the indices set of inactive, active and equality constraints and 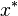 is an optimal solution of
is an optimal solution of  , then there exists a non-zero vector
, then there exists a non-zero vector ![\lambda=[\lambda_0, \lambda _1, \lambda _2,\dots,\lambda _n]](../I/m/33bd5d70c5e5bb8e148c73838383d960.png) such that:
such that:
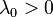 if the
if the 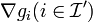 and
and 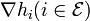 are linearly independent or, more generally, when a constraint qualification holds.
are linearly independent or, more generally, when a constraint qualification holds.
Named after Fritz John, these conditions are equivalent to the Karush–Kuhn–Tucker conditions in the case 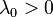 .
.
References
- WANG Yiju, XIU Naihua. 非线性规划的理论和方法 (The theory and methods of the Non-linear programming) (in Chinese). p. 4. ISBN 978-7-5369-3825-0.
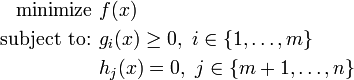
![\begin{cases}
\lambda_0 \nabla f(x^*) = \sum\limits_{i\in \mathcal{I}'} \lambda_i \nabla g_i(x^*) + \sum\limits_{i\in \mathcal{E}} \lambda_i \nabla h_i (x^*) \\[10pt]
\lambda_i \ge 0,\ i\in \mathcal{I}'\cup\{0\} \\[10pt]
\exists i\in \left( \{0,1,\ldots ,n\} \backslash \mathcal{I} \right) \left( \lambda_i \ne 0 \right)
\end{cases}](../I/m/eca2505019ca625515b1f72fb4d6f591.png)