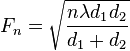Fresnel zone

In optics and radio communications (indeed, in any situation involving the radiation of waves, which includes electrodynamics, acoustics, gravitational radiation and seismology), a Fresnel zone (/freɪˈnɛl/ fray-NEL), named for physicist Augustin-Jean Fresnel, is one of a (theoretically infinite) number of concentric ellipsoids which define volumes in the radiation pattern of a (usually) circular aperture. Fresnel zones result from diffraction by the circular aperture.[1] The cross section of the first (innermost) Fresnel zone is circular. Subsequent Fresnel zones are annular (doughnut-shaped) in cross section, and concentric with the first.
Importance of Fresnel zones
If unobstructed, radio waves will travel in a straight line from the transmitter to the receiver. But if there are reflective surfaces along the path, such as bodies of water or smooth terrain, the radio waves reflecting off those surfaces may arrive either out of phase or in phase with the signals that travel directly to the receiver. Waves that reflect off of surfaces within an even Fresnel zone are out of phase with the direct-path wave and reduce the power of the received signal. Waves that reflect off of surfaces within an odd Fresnel zone are in phase with the direct-path wave and can enhance the power of the received signal. Sometimes this results in the counter-intuitive finding that reducing the height of an antenna increases the signal-to-noise ratio.
Fresnel provided a means to calculate where the zones are--where a given obstacle will cause mostly in phase or mostly out of phase reflections between the transmitter and the receiver. Obstacles in the first Fresnel zone will create signals with a path-length phase shift of 0 to 180 degrees, in the second zone they will be 180 to 360 degrees out of phase, and so on. Even numbered zones have the maximum phase cancelling effect and odd numbered zones may actually add to the signal power.[2]
To maximize receiver strength, one needs to minimize the effect of obstruction loss by removing obstacles from the radio frequency line of sight (RF LoS). The strongest signals are on the direct line between transmitter and receiver and always lie in the first Fresnel zone.
Determining Fresnel zone clearance

The concept of Fresnel zone clearance may be used to analyze interference by obstacles near the path of a radio beam. The first zone must be kept largely free from obstructions to avoid interfering with the radio reception. However, some obstruction of the Fresnel zones can often be tolerated. As a rule of thumb the maximum obstruction allowable is 40%, but the recommended obstruction is 20% or less.
For establishing Fresnel zones, first determine the RF Line of Sight (RF LoS), which in simple terms is a straight line between the transmitting and receiving antennas. Now the zone surrounding the RF LoS is said to be the Fresnel zone.[3]
The general equation for calculating the Fresnel zone radius at any point P in between the endpoints of the link is the following:
where,
Fn = The nth Fresnel Zone radius in metres
d1 = The distance of P from one end in metres
d2 = The distance of P from the other end in metres
 = The wavelength of the transmitted signal in metres
= The wavelength of the transmitted signal in metres
The cross sectional radius of each Fresnel zone is the longest at the midpoint of the RF LoS, shrinking to a point at the antenna on each end. For practical applications, it is often useful to know the maximum radius of the first Fresnel zone. From the above formula, the following formulas can be derived, using 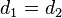 ,
, 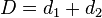 , and
, and 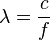 . Now we have an easy way to calculate the radius of the first Fresnel zone (F1 in the above equation), knowing the distance between the two antennas and the frequency of the transmitted signal.
. Now we have an easy way to calculate the radius of the first Fresnel zone (F1 in the above equation), knowing the distance between the two antennas and the frequency of the transmitted signal.
In SI:
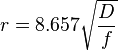
- where
- r = radius in metres
- D = total distance in kilometres
- f = frequency transmitted in gigahertz.
Or in imperial units:
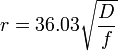
- where
- r = radius in feet
- D = total distance in miles
- f = frequency transmitted in Gigahertz.
See also
|
|
References
- ↑ "Fresnel zone". its.bldrdoc.gov. Retrieved 2008-02-21.
- ↑ "Wireless – Fresnel Zones and their Effect". zytrax.com. Retrieved 2008-02-21.
- ↑ "Fresnel Zone Clearance". softwright.com. Retrieved 2008-02-21.
 This article incorporates public domain material from the General Services Administration document "Federal Standard 1037C" (in support of MIL-STD-188).
This article incorporates public domain material from the General Services Administration document "Federal Standard 1037C" (in support of MIL-STD-188).