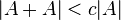Freiman's theorem

In mathematics, Freiman's theorem is a combinatorial result in number theory. In a sense it accounts for the approximate structure of sets of integers that contain a high proportion of their internal sums, taken two at a time.

The formal statement is:

Let A be a finite set of integers such that the sumset

is small, in the sense that

for some constant . There exists an n-dimensional arithmetic progression of length

that contains A, and such that c' and n depend only on c.^[1]

A simple instructive case is the following. We always have

 ≥ 

with equality precisely when A is an arithmetic progression.

This result is due to Gregory Freiman (1964,1966).^[2] Much interest in it, and applications, stemmed from a new proof by Imre Z. Ruzsa (1994).

See also

• Markov spectrum

References

• Freiman, G.A. (1964). "Addition of finite sets". Sov. Math., Dokl. (in English. Russian original) 5: 1366–1370. Zbl 0163.29501.  CS1 maint: Unrecognized language (link)
• Freiman, G. A. (1966). Foundations of a Structural Theory of Set Addition (in Russian). Kazan: Kazan Gos. Ped. Inst. p. 140. Zbl 0203.35305. 
• Freiman, G. A. (1999). "Structure theory of set addition". Astérisque 258: 1–33. Zbl 0958.11008. 
• Nathanson, Melvyn B. (1996). Additive Number Theory: Inverse Problems and Geometry of Sumsets. Graduate Texts in Mathematics 165. Springer. ISBN 0-387-94655-1. Zbl 0859.11003. 
• Ruzsa, Imre Z. (1994). "Generalized arithmetical progressions and sumsets". Acta Mathematica Hungarica 65 (4): 379–388. doi:10.1007/bf01876039. Zbl 0816.11008. 

This article incorporates material from Freiman's theorem on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.