Free spectral range

Free spectral range (FSR) is the spacing in optical frequency or wavelength between two successive reflected or transmitted optical intensity maxima or minima of an interferometer or diffractive optical element.

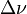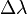The FSR is not always represented by $\Delta\nu$ or $\Delta\lambda$ , but instead is sometimes represented by just the letters FSR. The reason is because these difference terms often refer to the bandwidth or linewidth of an emitted source respectively.

In General

The free spectral range(FSR) of a cavity is given by:

\Delta\nu=\frac{c}{2n_gl}

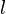Where $l$ is the length of the cavity, $n_g$ is the group index of the media within the cavity and $c$ is the speed of light.

In wavelength, the FSR is given by:

\Delta\lambda=\frac{\lambda^2}{2n_gl}

Where $\lambda$ is the vacuum wavelength of light in the cavity.

Diffraction gratings

The free spectral range of a diffraction grating is the largest wavelength range for a given order that does not overlap the same range in an adjacent order. If the (m+1)^th order of $\lambda$ and (m)^th order of $(\lambda + \Delta \lambda)$ lie at the same angle, then

\Delta \lambda={\lambda \over m}

Fabry–Pérot interferometer

In a Fabry–Pérot interferometer or etalon, the wavelength separation between adjacent transmission peaks is called the free spectral range of the etalon, and is given by:

\Delta\lambda = \frac{ \lambda_0^2}{2nl \cos\theta + \lambda_0 } \approx \frac{ \lambda_0^2}{2nl \cos\theta }

where λ₀ is the central wavelength of the nearest transmission peak, n is the index of refraction of the cavity medium, $\theta$ is the angle of incidence, and l is the thickness of the cavity. More often FSR is quoted in frequency, rather than wavelength units:

\Delta f \approx \frac{ c}{2nl \cos\theta }

The FSR is related to the full-width half-maximum, δλ, of any one transmission band by a quantity known as the finesse:

\mathcal{F} = \frac{\Delta\lambda}{\delta\lambda}=\frac{\pi}{2 \arcsin(1/\sqrt F)},

where $F = \frac{4R}{{(1-R)^2}}$ is the coefficient of finesse, and R is the reflectivity of the mirrors.

This is commonly approximated (for R > 0.5) by

\mathcal{F} \approx \frac{\pi \sqrt{F}}{2}=\frac{\pi R^{1/2} }{(1-R)}.