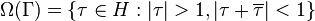Free regular set

In mathematics, a free regular set is a subset of a topological space that is acted upon disjointly under a given group action.[1]

To be more precise, let X be a topological space. Let G be a group of homeomorphisms from X to X. Then we say that the action of the group G at a point 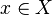x\in X is freely discontinuous if there exists a neighborhood U of x such that 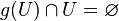g(U)\cap U=\varnothing for all 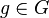g\in G, excluding the identity. Such a U is sometimes called a nice neighborhood of x.

The set of points at which G is freely discontinuous is called the free regular set and is sometimes denoted by 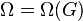\Omega=\Omega(G). Note that 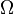\Omega is an open set.

If Y is a subset of X, then Y/G is the space of equivalence classes, and it inherits the canonical topology from Y; that is, the projection from Y to Y/G is continuous and open.

Note that 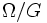\Omega /G is a Hausdorff space.

Examples

The open set

\Omega(\Gamma)=\{\tau\in H: |\tau|>1 , |\tau +\overline\tau| <1\}

is the free regular set of the modular group 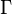\Gamma on the upper half-plane H. This set is called the fundamental domain on which modular forms are studied.

See also

References

  1. ↑ Maskit, Bernard (1987). Discontinuous Groups in the Plane, Grundlehren der mathematischen Wissenschaften Volume 287. Springer Berlin Heidelberg. pp. 15–16. ISBN 978-3-642-64878-6.