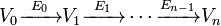Free category
In mathematics, the free category or path category generated by a directed graph or quiver is the category that results from freely concatenating arrows together, whenever the target of one arrow is the source of the next.
More precisely, the objects of the category are the vertices of the quiver, and the morphisms are paths between objects. Here, a path is defined as a sequence
where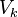 
is a vertex of the quiver, 
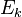is an edge of the quiver, and n ranges over the non-negative integers. The case of n=0 should be interpreted as the identity morphisms of the category.
Properties
The category of small categories Cat has a forgetful functor U into the quiver category Quiv:
- U : Cat → Quiv
This functor forgets the identity morphisms of a given category, and it forgets morphism compositions. A strict category is a category with the structure of Set; the idea of strictness here is to make sure that any chosen category has objects that can be interpreted as the vertices of a quiver, that is, where the equality of heads to tails of edges can be specified. The left adjoint of this functor is a functor F taking Quiv to the corresponding free categories, as defined above:
- F : Quiv → Cat
See also
- Free strict monoidal category