Fredkin gate
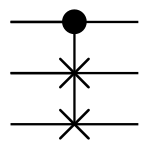
The Fredkin gate (also CSWAP gate) is a computational circuit suitable for reversible computing, invented by Ed Fredkin. It is universal, which means that any logical or arithmetic operation can be constructed entirely of Fredkin gates. The Fredkin gate is the three-bit gate that swaps the last two bits if the first bit is 1.
Definition
The basic Fredkin gate[1] is a controlled swap gate that maps three inputs (C, I1, I2) onto three outputs (C, O1, O2). The C input is mapped directly to the C output. If C = 0, no swap is performed; I1 maps to O1, and I2 maps to O2. Otherwise, the two outputs are swapped so that I1 maps to O2, and I2 maps to O1. It is easy to see that this circuit is reversible, i.e., "undoes" itself when run backwards. A generalized n×n Fredkin gate passes its first n-2 inputs unchanged to the corresponding outputs, and swaps its last two outputs if and only if the first n-2 inputs are all 1.
The Fredkin gate is the reversible three-bit gate that swaps the last two bits if the first bit is 1.
| Truth table | Matrix form | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
It has the useful property that the numbers of 0s and 1s are conserved throughout, which in the billiard ball model means the same number of balls are output as input. This corresponds nicely to the conservation of mass in physics, and helps to show that the model is not wasteful.
Logic function with XOR and AND gates
- O1 = I1 XOR S
- O2 = I2 XOR S
with S = (I1 XOR I2) AND C
It can also be implemented by the following logic:
- O1 = (NOT C AND I1) OR (C AND I2) = CI1+CI2
- O2 = (C AND I1) OR (NOT C AND I2) = CI1+CI2
- Cout= Cin
Completeness
One way to see that the Fredkin gate is universal is to observe that it can be used to implement AND and NOT:
- If
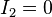 , then
, then 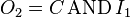 .
. - If
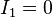 and
and 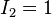 , then
, then 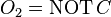 .
.
Example
Here is a diagram of a three-bit adder implemented using Fredkin gates. The three inputs are A, B and C, supplemented by the constant T and F. In the diagram, the leftmost input (before the colon) swaps the two rightmost inputs if it is true.
See also
- Quantum computing
- Quantum gate
- Quantum programming
- Toffoli gate, which is a controlled-controlled-NOT gate.
References
- ↑ Brown, Julian, The Quest for the Quantum Computer, New York : Touchstone, 2000.
Further reading
- Fredkin, Edward; Toffoli, Tommaso (1982). "Conservative Logic". International Journal of Theoretical Physics 21 (3-4): 219–253. doi:10.1007/BF01857727.
