Fred Galvin

Frederick William Galvin is a mathematician, currently a professor at the University of Kansas. His research interests include set theory and combinatorics.

His notable combinatorial work includes the proof of the Dinitz conjecture. In set theory, he proved with András Hajnal that if ℵω1 is a strong limit cardinal, then

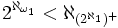
2^{\aleph_{\omega_1}}<\aleph_{(2^{\aleph_1})^+}

holds. The research on extending this result led Saharon Shelah to the invention of PCF theory. Galvin gave an elementary proof of the Baumgartner–Hajnal theorem 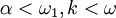\omega_1\to(\alpha)^2_k (\alpha<\omega_1, k<\omega). The original proof by Baumgartner and Hajnal used forcing and absoluteness. Galvin and Shelah also proved the square bracket partition relations \aleph_1\not\to[\aleph_1]^2_4 and 2^{\aleph_0}\not\to[2^{\aleph_0}]^2_{\aleph_0}. Galvin also proved the partition relation \eta\to[\eta]^2_3 where η denotes the order type of the set of rational numbers.

Galvin and Karel Prikry proved that every Borel set is Ramsey. Galvin and Komjáth showed that the axiom of choice is equivalent to the statement that every graph has a chromatic number.

Galvin received his Ph.D. in 1967 from the University of Minnesota.[1]

He invented doublemove chess.

References

  1. ↑ Fred Galvin at the Mathematics Genealogy Project