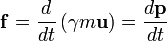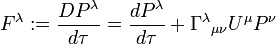Four-force
In the special theory of relativity four-force is a four-vector that replaces the classical force.
In Special Relativity
The four-force is the four-vector defined as the change in four-momentum over the particle's own time:
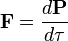 .
.
For a particle of constant invariant mass m > 0, 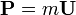 where
where 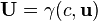 is the four-velocity, so we can relate the four-force with the four-acceleration
is the four-velocity, so we can relate the four-force with the four-acceleration 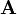 as in Newton's second law:
as in Newton's second law:
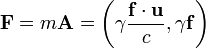 .
.
Here
and
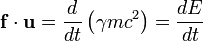 .
.
where 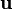 ,
, 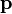 and
and 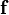 are 3-vectors describing the velocity and the momentum of the particle and the force acting on it respectively.
are 3-vectors describing the velocity and the momentum of the particle and the force acting on it respectively.
In General Relativity
In general relativity the relation between four-force, and four-acceleration remains the same, but the elements of the four-force are related to the elements of the four-momentum through a covariant derivative with respect to proper time.
In addition, we can formulate force using the concept of coordinate transformations between different coordinate systems. Assume that we know the correct expression for force in a coordinate system at which the particle is momentarily at rest. Then we can perform a transformation to another system to get the corresponding expression of force.[1] In special relativity the transformation will be a Lorentz transformation between coordinate systems moving with a relative constant velocity whereas in general relativity it will be a general coordinate transformation.
Consider the four-force 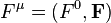 acting on a particle of mass
acting on a particle of mass 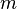 which is momentarily at rest in a coordinate system. The relativistic force
which is momentarily at rest in a coordinate system. The relativistic force 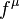 in another coordinate system moving with constant velocity
in another coordinate system moving with constant velocity 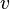 , relative to the other one, is obtained using a Lorentz transformation:
, relative to the other one, is obtained using a Lorentz transformation:
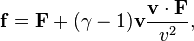
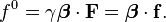
where 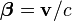 .
.
In general relativity, the expression for force becomes
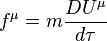
with covariant derivative 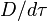 . The equation of motion becomes
. The equation of motion becomes
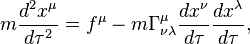
where 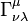 is the Christoffel symbol. If there is no external force, this becomes the equation for geodesics in the curved space-time. The second term in the above equation, plays the role of a gravitational force. If
is the Christoffel symbol. If there is no external force, this becomes the equation for geodesics in the curved space-time. The second term in the above equation, plays the role of a gravitational force. If 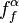 is the correct expression for force in a freely falling frame
is the correct expression for force in a freely falling frame 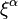 , we can use the then the equivalence principle to write the four-force in an arbitrary coordinate
, we can use the then the equivalence principle to write the four-force in an arbitrary coordinate 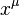 :
:
Examples
In special relativity, Lorentz 4-force (4-force acting to charged particle situated in electromagnetic field) can be expressed as:
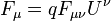 ,
,
where
-
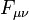 is electromagnetic tensor,
is electromagnetic tensor, -
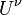 is 4-velocity, and
is 4-velocity, and -
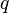 - electric charge.
- electric charge.
See also
References
- Rindler, Wolfgang (1991). Introduction to Special Relativity (2nd ed.). Oxford: Oxford University Press. ISBN 0-19-853953-3.