Foster's theorem
This article is about the theorem in Markov probability theory. For the theorem in electrical engineering, see Foster's reactance theorem.
In probability theory, Foster's theorem, named after F. G. Foster,[1] is used to draw conclusions about the positive recurrence of Markov chains with countable state spaces. It uses the fact that positive recurrent Markov chains exhibit a notion of "Lyapunov stability" in terms of returning to any state while starting from it within a finite time interval.
Consider an aperiodic, irreducible discrete-time Markov chain on a countable state space S having a transition probability matrix P with elements pij for pairs i, j in S. Foster's theorem states that the Markov chain is positive recurrent if and only if there exists a Lyapunov function V: S → R, such that 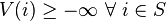 and
and
-
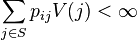 for
for 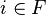
-
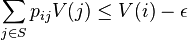 for all
for all 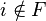
for some finite set F and strictly positive ε.[2]
Related links
References
- ↑ Foster, F. G. (1953). "On the Stochastic Matrices Associated with Certain Queuing Processes". The Annals of Mathematical Statistics 24 (3): 355. doi:10.1214/aoms/1177728976. JSTOR 2236286.
- ↑ Brémaud, P. (1999). "Lyapunov Functions and Martingales". Markov Chains. p. 167. doi:10.1007/978-1-4757-3124-8_5. ISBN 978-1-4419-3131-3.