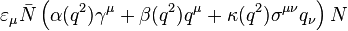Form factor (quantum field theory)

In mathematical physics, in particular in effective field theory, a form factor is a function that gives the properties of a certain particle interaction without including all of the underlying physics. It is measured experimentally when a theoretical calculation is unavailable or too difficult—see experimental particle physics.

Photon-nucleon example

For example, at low energies the interaction of a photon with a nucleon is a very complicated calculation involving interactions between the photon and a sea of quarks and gluons, and often the calculation cannot be done. Often in this context, form factors are also called "structure functions", since they can be used to describe the structure of the nucleon.

However the general form of the interaction is known,

\varepsilon_\mu \bar{N}\left(\alpha(q^2) \gamma^\mu + \beta(q^2) q^\mu + \kappa(q^2) \sigma^{\mu \nu} q_\nu \right)N \,

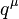where q^\mu represents the photon momentum (equal to E/c, where E is the energy of the photon). The three functions: 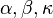\alpha, \beta , \kappa are the form factors for this interaction, they can be measured experimentally, and then the three effective vertices can be used to perform calculations that would otherwise be too difficult.

See also