Flat vector bundle

In mathematics, a vector bundle is said to be flat if it is endowed with an linear connection with vanishing curvature, ie. a flat connection.

de Rham cohomology of a flat vector bundle

Let 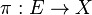$\pi:E \to X$ denote a flat vector bundle, and 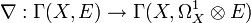$\nabla : \Gamma(X,E)\to \Gamma(X, \Omega_X^1\otimes E)$ be the covariant derivative associated to the flat connection on E.

Let 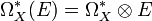$\Omega_X^* (E) = \Omega^*_X \otimes E$ denote the vector space (in fact a sheaf of modules over 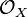$\mathcal O_X$ ) of differential forms on X with values in E. The covariant derivative defines a degree 1 endomorphism d, the differential of 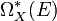$\Omega_X^* (E)$ , and the flatness condition is equivalent to the property $d^2 = 0$ .

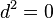In other words, the graded vector space 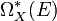$\Omega_X^* (E)$ is a cochain complex. Its cohomology is called the de Rham cohomology of E, or de Rham cohomology with coefficients twisted by the local coefficient system E.

Flat trivializations

A trivialization of a flat vector bundle is said to be flat if the connection form vanishes in this trivialization. An equivalent definition of a flat bundle is the choice of a trivializing atlas with locally constant transition maps.

Examples

Trivial line bundles can have several flat bundle structures. An example is the trivial bundle over 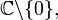$\mathbb C\backslash \{0\},$ with the connection forms 0 and 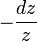$-\frac{dz}{z}$ . The parallel vector fields are constant in the first case, and proportional to local determinations of the complex logarithm in the second.

The real canonical line bundle 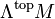$\Lambda^{\mathrm{top}}M$ of a differential manifold M is a flat line bundle, called the orientation bundle. Its sections are volume forms.

A Riemannian manifold is flat if, and only if, its Levi-Civita connection gives its tangent vector bundle a flat structure.

Flat vector bundle

de Rham cohomology of a flat vector bundle

Flat trivializations

Examples

See also