Flat manifold
In mathematics, a Riemannian manifold is said to be flat if its curvature is everywhere zero. Intuitively, a flat manifold is one that "locally looks like" Euclidean space in terms of distances and angles, e.g. the interior angles of a triangle add up to 180°.
The universal cover of a complete flat manifold is Euclidean space. This can be used to prove the theorem of Bieberbach (1911, 1912) that all compact flat manifolds are finitely covered by tori; the 3-dimensional case was proved earlier by Schoenflies (1891).
Examples
The following manifolds can be endowed with a flat metric. Note that this may not be their 'standard' metric (for example, the flat metric on the circle is not the metric induced by its embedding into 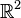 ).
).
Dimension 1
- The line
- The circle
Dimension 2
- The plane
- The cylinder
- The Moebius band
- The Klein bottle
- The 2-dimensional torus. A flat torus can be isometrically embedded in three-dimensional Euclidean space with a C1 map (by the Nash embedding theorem) but not with a C2 map, and the Clifford torus provides an isometric analytic embedding of a flat torus in four dimensions.
There are 17 compact 2-dimensional orbifolds with flat metric (including the torus and Klein bottle), listed in the article on orbifolds, that correspond to the 17 wallpaper groups.
Dimension 3
For the complete list of the 6 orientable and 4 non-orientable compact examples see Seifert fiber space.
Higher dimensions
- Euclidean space
- Tori
- Products of flat manifolds
- Quotients of flat manifolds by groups acting freely.
See also
- Space forms
- Crystallographic groups
- Ricci-flat manifold
- Conformally flat manifold
- Affine manifold
References
- Bieberbach, L. (1911), "Über die Bewegungsgruppen der Euklidischen Räume I", Mathematische Annalen 70 (3): 297–336, doi:10.1007/BF01564500.
- Bieberbach, L. (1912), "Über die Bewegungsgruppen der Euklidischen Räume II: Die Gruppen mit einem endlichen Fundamentalbereich", Mathematische Annalen 72 (3): 400–412, doi:10.1007/BF01456724.
- Schoenflies, A. (1891), Kristallsysteme und Kristallstruktur, Teubner.
- Vinberg, E.B. (2001), "Crystallographic group", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4