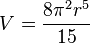Five-dimensional space

The idea of five-dimensional space is an abstraction which occurs frequently in mathematics, where it is a legitimate construct. (In physics and mathematics, a sequence of N numbers can be understood to represent a location in an N-dimensional space.) Whether or not the real universe in which we live is somehow five-dimensional is a topic that is debated and explored in several branches of physics, including astrophysics and particle physics.
Physics
In physics, the fifth dimension is a hypothetical extra dimension beyond the usual three spatial dimensions and one time dimension of Relativity. The Kaluza–Klein theory used the fifth dimension to unify gravity with the electromagnetic force. For example, Minkowski space and Maxwell's equations in vacuum can be embedded in a five-dimensional Riemann curvature tensor. Kaluza–Klein theory today is seen as essentially a gauge theory, with gauge group the circle group. M-theory suggests that space–time has 11 dimensions, seven of which are "rolled up" to below the subatomic level. Physicists have speculated that the graviton, a particle thought to carry the force of gravity, may "leak" into the fifth or higher dimensions, which would explain how gravity is significantly weaker than the other three fundamental forces.
In 1993, the physicist Gerard 't Hooft put forward the holographic principle, which explains that the information about an extra dimension is visible as a curvature in a spacetime with one fewer dimension. For example, holograms are three-dimensional pictures placed on a two-dimensional surface, which gives the image a curvature when the observer moves. Similarly, in general relativity, the fourth dimension is manifested in observable three dimensions as the curvature path of a moving infinitesimal (test) particle. Hooft has speculated that the fifth dimension is really the spacetime fabric.
Five-dimensional geometry
Polytopes
In five or more dimensions, only three regular polytopes exist. In five dimensions, they are:
- The 5-simplex of the simplex family, with 6 vertices, 15 edges, 20 faces (each an equilateral triangle), 15 cells (each a regular tetrahedron), and 6 hypercells (each a 5-cell).
- The 5-cube of the hypercube family, with 32 vertices, 80 edges, 80 faces (each a square), 40 cells (each a cube), and 10 hypercells (each a tesseract).
- The 5-orthoplex of the cross polytope family, with 10 vertices, 40 edges, 80 faces (each a triangle), 80 cells (each a tetrahedron), and 32 hypercells (each a 5-cell).
A fourth polytope, a demihypercube, can be constructed as an alternation of the 5-cube, and is called a 5-demicube, with half the vertices (16), bounded by alternating 5-cell and 16-cell hypercells.
| A5 | B5 | D5 | |
|---|---|---|---|
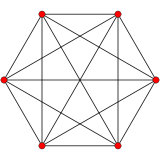 5-simplex |
 5-cube |
 5-orthoplex |
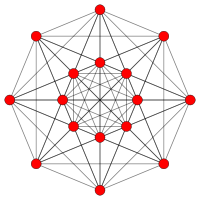 5-demicube |
Hypersphere
A hypersphere in 5-space (also called a 4-sphere due to its surface being 4-dimensional) consists of the set of all points in 5-space at a fixed distance r from a central point P. The hypervolume enclosed by this hypersurface is:
See also
- Higher dimension
- 5-manifold
- List of regular 5-polytopes
- Hypersphere
- Dimension
Further reading
- Wesson, Paul S. (1999). Space-Time-Matter, Modern Kaluza-Klein Theory. Singapore: World Scientific. ISBN 981-02-3588-7.
- Wesson, Paul S. (2006). Five-Dimensional Physics: Classical and Quantum Consequences of Kaluza-Klein Cosmology. Singapore: World Scientific. ISBN 981-256-661-9.
- Weyl, Hermann, Raum, Zeit, Materie, 1918. 5 edns. to 1922 ed. with notes by Jūrgen Ehlers, 1980. trans. 4th edn. Henry Brose, 1922 Space Time Matter, Methuen, rept. 1952 Dover. ISBN 0-486-60267-2.
External links
| |||||||||||||||||||||||||