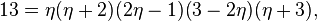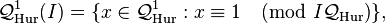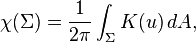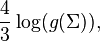First Hurwitz triplet

In the mathematical theory of Riemann surfaces, the first Hurwitz triplet is a triple of distinct Hurwitz surfaces with the identical automorphism group of the lowest possible genus, namely 14 (genera 3 and 7 each admit a unique Hurwitz surface, respectively the Klein quartic and the Macbeath surface). The explanation for this phenomenon is arithmetic. Namely, in the ring of integers of the appropriate number field, the rational prime 13 splits as a product of three distinct prime ideals. The principal congruence subgroups defined by the triplet of primes produce Fuchsian groups corresponding to the triplet of Riemann surfaces.

Arithmetic construction

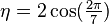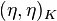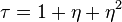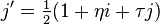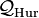Let $K$ be the real subfield of $\mathbb{Q}[\rho]$ where $\rho$ is a 7th-primitive root of unity. The ring of integers of K is $\mathbb{Z}[\eta]$ , where $\eta=2\cos(\tfrac{2\pi}{7})$ . Let $D$ be the quaternion algebra, or symbol algebra $(\eta,\eta)_{K}$ . Also Let $\tau=1+\eta+\eta^2$ and $j'=\tfrac{1}{2}(1+\eta i + \tau j)$ . Let $\mathcal{Q}_\mathrm{Hur}=\mathbb{Z}[\eta][i,j,j']$ . Then $\mathcal{Q}_\mathrm{Hur}$ is a maximal order of $D$ (see Hurwitz quaternion order), described explicitly by Noam Elkies [1].

In order to construct the first Hurwitz triplet, consider the prime decomposition of 13 in $\mathbb{Z}[\eta]$ , namely

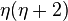13=\eta (\eta +2)(2\eta-1)(3-2\eta)(\eta+3),

where $\eta (\eta+2)$ is invertible. Also consider the prime ideals generated by the non-invertible factors. The principal congruence subgroup defined by such a prime ideal I is by definition the group \mathrm

\mathcal{Q}^1_\mathrm{Hur}(I) = \{x \in \mathcal{Q}_\mathrm{Hur}^1 : x \equiv 1 \pmod{I\mathcal{Q}_\mathrm{Hur}}\},

namely, the group of elements of reduced norm 1 in 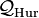$\mathcal{Q}_\mathrm{Hur}$ equivalent to 1 modulo the ideal 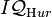$I\mathcal{Q}_{\mathrm Hur}$ . The corresponding Fuchsian group is obtained as the image of the principal congruence subgroup under a representation to PSL(2,R).

Each of the three Riemann surfaces in the first Hurwitz triplet can be formed as a Fuchsian model, the quotient of the hyperbolic plane by one of these three Fuchsian groups.

Bound for systolic length and the systolic ratio

The Gauss–Bonnet theorem states that

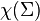\chi(\Sigma)=\frac{1}{2\pi} \int_{\Sigma} K(u)\,dA,

where $\chi(\Sigma)$ is the Euler characteristic of the surface and 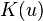$K(u)$ is the Gaussian curvature . In the case 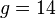$g=14$ we have

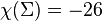\chi(\Sigma)=-26

and

K(u)=-1,

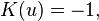
thus we obtain that the area of these surfaces is

52\pi

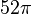The lower bound on the systole as specified in [2], namely

\frac{4}{3} \log(g(\Sigma)),

is 3.5187.

Some specific details about each of the surfaces are presented in the following tables (the number of systolic loops is taken from [3]).The term Systolic Trace refers to the least reduced trace of an element in the corresponding subgroup 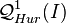$\mathcal{Q}^1_{Hur}(I)$ . The systolic ratio is the ratio of the square of the systole to the area.

Ideal	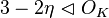$3-2\eta\vartriangleleft O_K$
Systole	5.9039
Systolic Trace	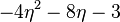$-4\eta^2-8\eta-3$
Systolic Ratio	0.2133
Number of Systolic Loops	91

Ideal	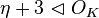$\eta+3 \vartriangleleft O_K$
Systole	6.3933
Systolic Trace	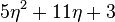$5\eta^2+11\eta+3$
Systolic Ratio	0.2502
Number of Systolic Loops	78

Ideal	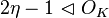$2\eta-1 \vartriangleleft O_K$
Systole	6.8879
Systolic Trace	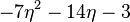$-7\eta^2-14\eta-3$
Systolic Ratio	0.2904
Number of Systolic Loops	364

References

Elkies, N. (1999). The Klein quartic in number theory. The eightfold way. Math. Sci. Res. Inst. Publ. 35. Cambridge: Cambridge Univ. Press. pp. 51–101.
Katz, M.; Schaps, M.; Vishne, U. (2007). "Logarithmic growth of systole of arithmetic Riemann surfaces along congruence subgroups". J. Differential Geom. 76: 399–422. arXiv:math.DG/0505007.
Vogeler, R. (2003). "On the geometry of Hurwitz surfaces". Thesis. Florida State University.

First Hurwitz triplet

Arithmetic construction

Bound for systolic length and the systolic ratio

See also

References