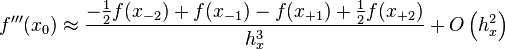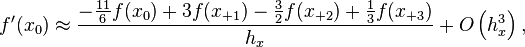Finite difference coefficient

In mathematics, to approximate a derivative to an arbitrary order of accuracy, it is possible to use the finite difference. A finite difference can be central, forward or backward.

Central finite difference

This table contains the coefficients of the central differences, for several orders of accuracy:[1]

Derivative Accuracy −4 −3 −2 −1 0 1 2 3 4
1 2       −1/2 0 1/2      
4     1/12 −2/3 0 2/3 −1/12    
6   −1/60 3/20 −3/4 0 3/4 −3/20 1/60  
8 1/280 −4/105 1/5 −4/5 0 4/5 −1/5 4/105 −1/280
2 2       1 −2 1      
4     −1/12 4/3 −5/2 4/3 −1/12    
6   1/90 −3/20 3/2 −49/18 3/2 −3/20 1/90  
8 −1/560 8/315 −1/5 8/5 −205/72 8/5 −1/5 8/315 −1/560
3 2     −1/2 1 0 −1 1/2    
4   1/8 −1 13/8 0 −13/8 1 −1/8  
6 −7/240 3/10 −169/120 61/30 0 −61/30 169/120 −3/10 7/240
4 2     1 −4 6 −4 1    
4   −1/6 2 −13/2 28/3 −13/2 2 −1/6  
6 7/240 −2/5 169/60 −122/15 91/8 −122/15 169/60 −2/5 7/240
5 2   −1/2 2 −5/2 0 5/2 −2 1/2  
6 2   1 −6 15 −20 15 −6 1  

For example, the third derivative with a second-order accuracy is

\displaystyle f'''(x_{0}) \approx \displaystyle \frac{-\frac{1}{2}f(x_{-2}) + f(x_{-1}) -f(x_{+1}) +\frac{1}{2}f(x_{+2})}{h^3_x} + O\left(h_x^2 \right)

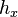where h_x represents a uniform grid spacing between each finite difference interval.

Forward and backward finite difference

This table contains the coefficients of the forward differences, for several order of accuracy:[1]

Derivative Accuracy 0 1 2 3 4 5 6 7 8
1 1 −1 1              
2 −3/2 2 −1/2            
3 −11/6 3 −3/2 1/3          
4 −25/12 4 −3 4/3 −1/4        
5 −137/60 5 −5 10/3 −5/4 1/5      
6 −49/20 6 −15/2 20/3 −15/4 6/5 −1/6    
2 1 1 −2 1            
2 2 −5 4 −1          
3 35/12 −26/3 19/2 −14/3 11/12        
4 15/4 −77/6 107/6 −13 61/12 −5/6      
5 203/45 −87/5 117/4 −254/9 33/2 −27/5 137/180    
6 469/90 −223/10 879/20 −949/18 41 −201/10 1019/180 −7/10  
3 1 −1 3 −3 1          
2 −5/2 9 −12 7 −3/2        
3 −17/4 71/4 −59/2 49/2 −41/4 7/4      
4 −49/8 29 −461/8 62 −307/8 13 −15/8    
5 −967/120 638/15 −3929/40 389/3 −2545/24 268/5 −1849/120 29/15  
6 −801/80 349/6 −18353/120 2391/10 −1457/6 4891/30 −561/8 527/30 −469/240
4 1 1 −4 6 −4 1        
2 3 −14 26 −24 11 −2      
3 35/6 −31 137/2 −242/3 107/2 −19 17/6    
4 28/3 −111/2 142 −1219/6 176 −185/2 82/3 −7/2  
5 1069/80 −1316/15 15289/60 −2144/5 10993/24 −4772/15 2803/20 −536/15 967/240

For example, the first derivative with a third-order accuracy and the second derivative with a second-order accuracy are

\displaystyle f'(x_{0}) \approx \displaystyle \frac{-\frac{11}{6}f(x_{0}) + 3f(x_{+1}) -\frac{3}{2}f(x_{+2}) +\frac{1}{3}f(x_{+3}) }{h_{x}} + O\left(h_{x}^3 \right),
\displaystyle f''(x_{0}) \approx \displaystyle \frac{2f(x_{0}) - 5f(x_{+1}) + 4f(x_{+2}) - f(x_{+3}) }{h_{x}^2} + O\left(h_{x}^2 \right),

while the corresponding backward approximations are given by

\displaystyle f'(x_{0}) \approx \displaystyle \frac{\frac{11}{6}f(x_{0}) - 3f(x_{-1}) +\frac{3}{2}f(x_{-2}) -\frac{1}{3}f(x_{-3}) }{h_{x}} + O\left(h_{x}^3 \right),
\displaystyle f''(x_{0}) \approx \displaystyle \frac{2f(x_{0}) - 5f(x_{-1}) + 4f(x_{-2}) - f(x_{-3}) }{h_{x}^2} + O\left(h_{x}^2 \right),


In general, to get the coefficients of the backward approximations, give all odd derivatives listed in the table the opposite sign, whereas for even derivatives the signs stay the same. The following table illustrates this:

Derivative Accuracy −8 −7 −6 −5 −4 −3 −2 −1 0
1 1               −1 1
2             1/2 −2 3/2
2 1             1 −2 1
2           −1 4 −5 2
3 1           −1 3 −3 1
2         3/2 −7 12 −9 5/2
4 1         1 −4 6 −4 1
2       −2 11 −24 26 −14 3

See also

References

  1. ↑ 1.0 1.1 Fornberg, Bengt (1988), "Generation of Finite Difference Formulas on Arbitrarily Spaced Grids", Mathematics of Computation 51 (184): 699–706, doi:10.1090/S0025-5718-1988-0935077-0, ISSN 0025-5718.