Finite character
In mathematics, a family  of sets is of finite character provided it has the following properties:
of sets is of finite character provided it has the following properties:
- For each
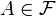 , every finite subset of
, every finite subset of  belongs to
belongs to  .
. - If every finite subset of a given set
 belongs to
belongs to  , then
, then  belongs to
belongs to  .
.
Properties
A family  of sets of finite character enjoys the following properties:
of sets of finite character enjoys the following properties:
- For each
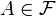 , every (finite or infinite) subset of
, every (finite or infinite) subset of  belongs to
belongs to  .
. - Tukey's lemma: In
 , partially ordered by inclusion, the union of every chain of elements of
, partially ordered by inclusion, the union of every chain of elements of  also belong to
also belong to  , therefore, by Zorn's lemma,
, therefore, by Zorn's lemma,  contains at least one maximal element.
contains at least one maximal element.
Example
Let V be a vector space, and let F be the family of linearly independent subsets of V. Then F is a family of finite character (because a subset X ⊆ V is linearly dependent iff X has a finite subset which is linearly dependent). Therefore, in every vector space, there exists a maximal family of linearly independent elements. As a maximal family is a vector basis, every vector space has a (possibly infinite) vector basis.
This article incorporates material from finite character on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.