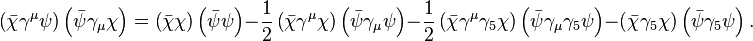Fierz identity
In theoretical physics, a Fierz identity is an identity that allows one to rewrite bilinears of the product of two spinors as a linear combination of products of the bilinears of the individual spinors. It is named after Swiss physicist Markus Fierz.
There is a version of the Fierz identities for Dirac spinors and there is another version for Weyl spinors. And there are versions for other dimensions besides 3+1 dimensions.
Spinor bilinears can be thought of as elements of a Clifford Algebra. Then the Fierz identity is the concrete realization of the relation to the exterior algebra. The identities for a generic scalar written as the contraction of two Dirac bilinears of the same type can be written with coefficients according the following table.
| Product | S | V | T | A | P | |
|---|---|---|---|---|---|---|
| S × S = | 1/4 | 1/4 | -1/4 | -1/4 | 1/4 | |
| V × V = | 1 | -1/2 | 0 | -1/2 | -1 | |
| T × T = | -3/2 | 0 | -1/2 | 0 | -3/2 | |
| A × A = | -1 | -1/2 | 0 | -1/2 | 1 | |
| P × P = | 1/4 | -1/4 | -1/4 | 1/4 | 1/4 | |
For example the V × V product can be expanded as,
Simplifications arise when the considered spinors are chiral or Majorana spinors as some term in the expansion can be vanishing.
References
A derivation of identities for rewriting any scalar contraction of Dirac bilinears can be found in 29.3.4 of L. B. Okun (1980). Leptons and Quarks. North-Holland. ISBN 978-0-444-86924-1.
See also appendix B.1.2 in T. Ortin (2004). Gravity and Strings. Cambridge University Press. ISBN 978-0-521-82475-0.