Fibonacci word
A Fibonacci word is a specific sequence of binary digits (or symbols from any two-letter alphabet). The Fibonacci word is formed by repeated concatenation in the same way that the Fibonacci numbers are formed by repeated addition.
It is a paradigmatic example of a Sturmian word.
The name “Fibonacci word” has also been used to refer to the members of a formal language L consisting of strings of zeros and ones with no two repeated ones. Any prefix of the specific Fibonacci word belongs to L, but so do many other strings. L has a Fibonacci number of members of each possible length.
Definition
Let 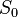 be "0" and
be "0" and 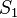 be "01". Now
be "01". Now 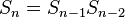 (the concatenation of the previous sequence and the one before that).
(the concatenation of the previous sequence and the one before that).
The infinite Fibonacci word is the limit 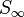 .
.
The Fibonacci words
We have:
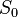 0
0
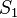 01
01
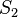 010
010
 01001
01001
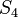 01001010
01001010
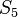 0100101001001
0100101001001
...
The first few elements of the infinite Fibonacci word are:
0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, ... (sequence A003849 in OEIS)
Closed-form expression for individual digits
The nth digit of the word is 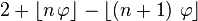 where
where 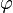 is the golden ratio and
is the golden ratio and  is the floor function (sequence A003849 in OEIS).
is the floor function (sequence A003849 in OEIS).
Substitution rules
Another way of going from Sn to Sn + 1 is to replace each symbol 0 in Sn with the pair of consecutive symbols 0, 1 in Sn + 1, and to replace each symbol 1 in Sn with the single symbol 0 in Sn + 1.
Alternatively, one can imagine directly generating the entire infinite Fibonacci word by the following process: start with a cursor pointing to the single digit 0. Then, at each step, if the cursor is pointing to a 0, append 1, 0 to the end of the word, and if the cursor is pointing to a 1, append 0 to the end of the word. In either case, complete the step by moving the cursor one position to the right.
A similar infinite word, sometimes called the rabbit sequence, is generated by a similar infinite process with a different replacement rule: whenever the cursor is pointing to a 0, append 1, and whenever the cursor is pointing to a 1, append 0, 1. The resulting sequence begins
- 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, ...
However this sequence differs from the Fibonacci word only trivially, by swapping 0s for 1s and shifting the positions by one.
A closed form expression for the so-called rabbit sequence:
The nth digit of the word is 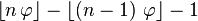 where
where 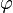 is the golden ratio and
is the golden ratio and  is the floor function.
is the floor function.
Discussion
The word is related to the famous sequence of the same name (the Fibonacci sequence) in the sense that addition of integers in the inductive definition is replaced with string concatenation. This causes the length of Sn to be Fn + 2, the (n + 2)th Fibonacci number. Also the number of 1s in Sn is Fn and the number of 0s in Sn is Fn + 1.
Other properties
- The infinite Fibonacci word is not periodic and not ultimately periodic.
- The last two letters of a Fibonacci word are alternately "01" and "10".
- Suppressing the last two letters of a Fibonacci word, or prefixing the complement of the last two letters, creates a palindrome. Example: 01
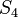 = 0101001010 is a palindrome. The palindromic density of the infinite Fibonacci word is thus 1/φ, where φ is the Golden ratio: this is the largest possible value for aperiodic words.[1]
= 0101001010 is a palindrome. The palindromic density of the infinite Fibonacci word is thus 1/φ, where φ is the Golden ratio: this is the largest possible value for aperiodic words.[1] - In the infinite Fibonacci word, the ratio (number of letters)/(number of zeroes) is φ, as is the ratio of zeroes to ones.
- The infinite Fibonacci word is a balanced sequence: Take two factors of the same length anywhere in the Fibonacci word. The difference between their Hamming weights (the number of occurrences of "1") never exceeds 1.[2]
- The subwords 11 and 000 never occur.
- The complexity function of the infinite Fibonacci word is n+1: it contains n+1 distinct subwords of length n. Example: There are 4 distinct subwords of length 3 : "001", "010", "100" and "101". Being also non-periodic, it is then of "minimal complexity", and hence a Sturmian word,[3] with slope
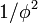 . The infinite Fibonacci word is the standard word generated by the directive sequence (1,1,1,....).
. The infinite Fibonacci word is the standard word generated by the directive sequence (1,1,1,....). - The infinite Fibonacci word is recurrent; that is, every subword occurs infinitely often.
- If
 is a subword of the infinite Fibonacci word, then so is its reversal, denoted
is a subword of the infinite Fibonacci word, then so is its reversal, denoted 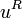 .
. - If
 is a subword of the infinite Fibonacci word, then the least period of
is a subword of the infinite Fibonacci word, then the least period of  is a Fibonacci number.
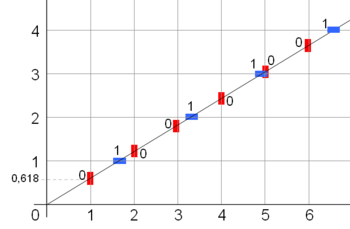
is a Fibonacci number. - The concatenation of two successive Fibonacci words is "almost commutative".
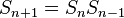 and
and 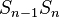 differ only by their last two letters.
differ only by their last two letters. - As a consequence, the infinite Fibonacci word can be characterized by a cutting sequence of a line of slope
 or
or 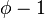 . See figure above.
. See figure above. - The number 0.010010100..., whose decimals are built with the digits of the infinite Fibonacci word, is transcendental.
- The letters "1" can be found at the positions given by the successive values of the Upper Wythoff sequence (OEIS A001950):
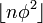
- The letters "0" can be found at the positions given by the successive values of the Lower Wythoff sequence (OEIS A000201):
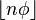
- The infinite Fibonacci word can contain repetitions of 3 successive identical subwords, but never 4. The critical exponent for the infinite Fibonacci word is
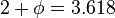 repetitions.[4] It is the smallest index (or critical exponent) among all Sturmian words.
repetitions.[4] It is the smallest index (or critical exponent) among all Sturmian words. - The infinite Fibonacci word is often cited as the worst case for algorithms detecting repetitions in a string.
- The infinite Fibonacci word is a morphic word, generated in {0,1}∗ by the endomorphism 0 → 01, 1 → 0.[5]
Applications
Fibonacci based constructions are currently used to model physical systems with aperiodic order such as quasicrystals. Crystal growth techniques have been used to grow Fibonacci layered crystals and study their light scattering properties.[6]
See also
- Tribonacci word
Notes
- ↑ Adamczewski, Boris; Bugeaud, Yann (2010), "8. Transcendence and diophantine approximation", in Berthé, Valérie; Rigo, Michael, Combinatorics, automata, and number theory, Encyclopedia of Mathematics and its Applications 135, Cambridge: Cambridge University Press, p. 443, ISBN 978-0-521-51597-9, Zbl pre05879512
- ↑ Lothaire (2011), p. 47.
- ↑ de Luca (1995).
- ↑ Allouche & Shallit (2003), p. 37.
- ↑ Lothaire (2011), p. 11.
- ↑ Dharma-wardana et al. (1987).
References
- Allouche, Jean-Paul; Shallit, Jeffrey (2003), Automatic Sequences: Theory, Applications, Generalizations, Cambridge University Press, ISBN 978-0-521-82332-6.
- Dharma-wardana, M. W. C.; MacDonald, A. H.; Lockwood, D. J.; Baribeau, J.-M.; Houghton, D. C. (1987), "Raman scattering in Fibonacci superlattices", Physical Review Letters 58: 1761–1765, doi:10.1103/physrevlett.58.1761.
- Lothaire, M. (1997), Combinatorics on Words, Encyclopedia of Mathematics and Its Applications 17 (2nd ed.), Cambridge University Press, ISBN 0-521-59924-5.
- Lothaire, M. (2011), Algebraic Combinatorics on Words, Encyclopedia of Mathematics and Its Applications 90, Cambridge University Press, ISBN 978-0-521-18071-9. Reprint of the 2002 hardback.
- de Luca, Aldo (1995), "A division property of the Fibonacci word", Information Processing Letters 54 (6): 307–312, doi:10.1016/0020-0190(95)00067-M.
- Mignosi, F.; Pirillo, G. (1992), "Repetitions in the Fibonacci infinite word", Informatique théorique et application 26 (3): 199–204.
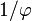 or
or 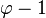 , with
, with