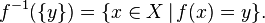Fiber (mathematics)

In mathematics, the term fiber (or fibre in British English) can have two meanings, depending on the context:

  1. In naive set theory, the fiber of the element y in the set Y under a map f : X → Y is the inverse image of the singleton \{y\} under f.
  2. In algebraic geometry, the notion of a fiber of a morphism of schemes must be defined more carefully because, in general, not every point is closed.

Definitions

Fiber in naive set theory

Let f : X → Y be a map. The fiber of an element 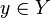y \in Y, commonly denoted by 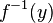f^{-1}(y), is defined as

f^{-1}(\{y\})=\{x \in X \, | \, f(x) = y\}.

In various applications, this is also called:

  • the inverse image of \{y\} under the map f
  • the preimage of \{y\} under the map f
  • the level set of the function f at the point y.

The term level set is only used if f maps into the real numbers and so y is simply a number. If f is a continuous function and if y is in the image of f, then the level set of y under f is a curve in 2D, a surface in 3D, and more generally a hypersurface of dimension d-1.

Fiber in algebraic geometry

In algebraic geometry, if f : X → Y is a morphism of schemes, the fiber of a point p in Y is the fibered product X\times_Y \mathrm{Spec}\, k(p) where k(p) is the residue field at p.

Terminological variance

The recommended practice is to use the terms fiber, inverse image, preimage, and level set as follows:

  • the fiber of the element y under the map f
  • the inverse image of the set \{y\} under the map f
  • the preimage of the set \{y\} under the map f
  • the level set of the function f at the point y.

By abuse of language, the following terminology is sometimes used but should be avoided:

  • the fiber of the map f at the element y
  • the inverse image of the map f at the element y
  • the preimage of the map f at the element y
  • the level set of the point y under the map f.

See also