Feynman parametrization
Feynman parametrization is a technique for evaluating loop integrals which arise from Feynman diagrams with one or more loops. However, it is sometimes useful in integration in areas of pure mathematics as well.
Richard Feynman observed that:
which simplifies evaluating integrals like:
More generally, using the Dirac delta function:
Even more generally, provided that 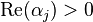 for all
for all 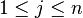 :
:
See also Schwinger parametrization.
Derivation
Now just linearly transform the integral using the substitution,
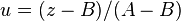 which leads to
which leads to 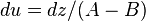 so
so 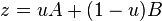
and we get the desired result:
In more general cases, derivations can be done very efficiently using the Schwinger parametrization. For example, in order to derive the Feynman parametrized form of :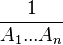 , we first reexpress all the factors in the denominator in their Schwinger parametrized form:
, we first reexpress all the factors in the denominator in their Schwinger parametrized form:
and rewrite,
Then we perform the following change of integration variables,
to obtain,
The next step is to perform the  integration.
integration.
where we have defined 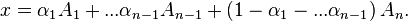
Substituting this result, we get to the penultimate form,
and, after introducing an extra integral, we arrive at the final form of the Feynman parametrization, namely,
Similarly, in order to derive the Feynman parametrization form of the most general case, :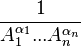 one could begin with the suitable different Schwinger parametrization form of factors in the denominator, namely,
one could begin with the suitable different Schwinger parametrization form of factors in the denominator, namely,
and then proceed exactly along the lines of previous case.
Symmetric form
A symmetric form of the parametrization is occasionally used, where the integral is instead performed on the interval ![[-1,1]](../I/m/d060b17b29e0dae91a1cac23ea62281a.png) , leading to:
, leading to:
References
- ↑ Kristjan Kannike. "Notes on Feynman Parametrization and the Dirac Delta Function" (PDF). Archived from the original (PDF) on 2007-07-29. Retrieved 2011-07-24.
![\frac{1}{AB}=\int^1_0 \frac{du}{\left[uA +(1-u)B\right]^2}](../I/m/b01075c7b68a9176b1e228b7fcd7bce3.png)
![\int \frac{dp}{A(p)B(p)}=\int dp \int^1_0 \frac{du}{\left[uA(p)+(1-u)B(p)\right]^2}=\int^1_0 du \int \frac{dp}{\left[uA(p)+(1-u)B(p)\right]^2}.](../I/m/221fd349d1ff7abd187b5f2088983fdc.png)
![\begin{align}
\frac{1}{A_1\cdots A_n}&=(n-1)!\int^1_0 du_1 \cdots \int^1_0 du_n \frac{\delta(u_1+\dots+u_n-1)}{\left[u_1 A_1+\dots +u_n A_n\right]^n} \\
&=(n-1)! \int^1_0 du_1 \int^{u_1}_0 du_2 \cdots \int^{u_{n-2}}_0 du_{n-1} \frac{1}{\left[A_1+u_1(A_2-A_1)+\dots+u_{n-1} (A_n-A_{n-1})\right]^n}.
\end{align}](../I/m/932b4c66c32eeb88d0c61bf572946c6a.png)
![\frac{1}{A_{1}^{\alpha_{1}}\cdots A_{n}^{\alpha_{n}}}=\frac{\Gamma(\alpha_{1}+\dots+\alpha_{n})}{\Gamma(\alpha_{1})\cdots\Gamma(\alpha_{n})}\int_{0}^{1}du_{1}\cdots\int_{0}^{1}du_{n}\frac{\delta(\sum_{k=1}^{n}u_{k}-1)u_{1}^{\alpha_{1}-1}\cdots u_{n}^{\alpha_{n}-1}}{\left[u_{1}A_{1}+\cdots+u_{n}A_{n}\right]^{\sum_{k=1}^{n}\alpha_{k}}}
.](../I/m/ed250f9efc19561dfc065de1fc4da0aa.png)
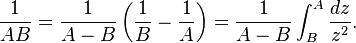
![\frac{1}{AB} = \int_0^1 \frac{du}{\left[uA + (1-u)B\right]^2}.](../I/m/09a81701136930c16181297de5c559a9.png)
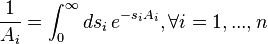
![\frac{1}{A_1...A_n}=\int_0^\infty ds_1...ds_n \exp\left[-\left(s_1A_1+...s_nA_n\right)\right].](../I/m/f6fe2db4fee7aa21a313c6dddae95262.png)
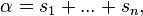
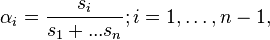
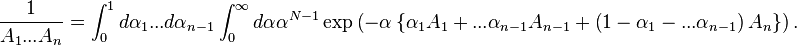
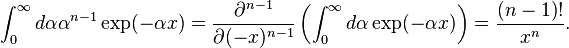
![\frac{1}{A_1...A_n}=\left(n-1\right)!\int_{0}^{1}d\alpha_1...d\alpha_{n-1}\frac{1}{[\alpha_1A_1+...+\alpha_{n-1}A_{n-1}+ \left(1-\alpha_{1}-...\alpha_{n-1}\right)A_{n}]^n} ,](../I/m/dd818172a0fe3d879979a0c0833260af.png)
![\frac{1}{A_1...A_n}=\left(n-1\right)!\int_{0}^{1}d\alpha_1...d\alpha_{n}\frac{\delta\left(1-\alpha_1-...-\alpha_n\right)}{[\alpha_1A_1+...+\alpha_{n}A_{n}]^n} .](../I/m/ef26e2bf645fe00cace97f71ffa5d1f8.png)
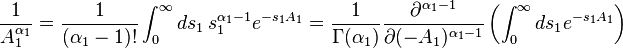
![\frac{1}{AB} = 2\int_{-1}^1 \frac{du}{\left[(1+u)A + (1-u)B\right]^2}.](../I/m/9dccb31c821b3e42f25d7f47444c998d.png)