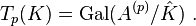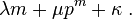Ferrero–Washington theorem

In algebraic number theory, the Ferrero–Washington theorem, proved first by Ferrero & Washington (1979) and later by Sinnott (1984), states that Iwasawa's μ-invariant vanishes for cyclotomic Zp-extensions of abelian algebraic number fields.

History

Iwasawa (1959) introduced the μ-invariant of a Zp-extension and observed that it was zero in all cases he calculated. Iwasawa & Sims (1966) used a computer to check that it vanishes for the cyclotomic Zp-extension of the rationals for all primes less than 4000. Iwasawa (1971) later conjectured that the μ-invariant vanishes for any Zp-extension, but shortly after Iwasawa (1973) discovered examples of non-cyclotomic extensions of number fields with non-vanishing μ-invariant showing that his original conjecture was wrong. He suggested, however, that the conjecture might still hold for cyclotomic Zp-extensions.

Iwasawa (1958) showed that the vanishing of the μ-invariant for cyclotomic Zp-extensions of the rationals is equivalent to certain congruences between Bernoulli numbers, and Ferrero & Washington (1979) showed that the μ-invariant vanishes in these cases by proving that these congruences hold.

Statement

For a number field K we let Km denote the extension by pm-power roots of unity, 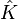\hat K the union of the Km and A(p) the maximal unramified abelian p-extension of 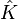\hat K. Let the Tate module

T_p(K) = \mathrm{Gal}(A^{(p)}/\hat K) \ .

Then Tp(K) is a pro-p-group and so a Zp-module. Using class field theory one can describe Tp(K) as isomorphic to the inverse limit of the class groups Cm of the Km under norm.[1]

Iwasawa exhibited Tp(K) as a module over the completion Zp[[T]] and this implies a formula for the exponent of p in the order of the class groups Cm of the form

\lambda m + \mu p^m + \kappa \ .

The Ferrero–Washington theorem states that μ is zero.[2]

References

  1. ↑ Manin & Panchishkin 2007, p. 245
  2. ↑ Manin & Panchishkin 2007, p. 246