Fermi heap and Fermi hole

Fermi heap and Fermi hole refer to two closely related quantum phenomena that occur in many-electron atoms. They arise due to the Pauli exclusion principle, according to which no two electrons can be in the same quantum state in a system (which, accounting for electrons' spin, means that there can be up to two electrons in the same orbital). Due to indistinguishability of elementary particles, the probability of a measurement yielding a certain eigenvalue must be invariant when electrons are exchanged, which means that the probability amplitude must either remain the same or change sign. For instance, consider an excited state of the helium atom in which electron 1 is in the 1s orbital and electron 2 has been excited to the 2s orbital. It is not possible, even in principle, to distinguish electron 1 from electron 2. In other words, electron 2 might be in the 1s orbital with electron 1 in the 2s orbital. As they are fermions, electrons must be described by an anti-symmetric wavefunction which must change sign under electron exchange, resulting in either a Fermi hole (having a lower probability of being found close to each other) or a Fermi heap (having a higher probability of being found close to each other). Since electrons repel one another electrically, Fermi holes and Fermi heaps have drastic effects on the energy of many-electron atoms, although the effect can be illustrated in the case of the helium atom.

Neglecting the spin-orbit interaction, the wavefunction for the two electrons can be written as 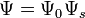$\Psi = \Psi_0 \Psi_s$ , where we have split the wavefunction into spatial and spin parts. As mentioned above, 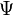$\Psi$ needs to be antisymmetric, and so the antisymmetry can arise either from the spin part or the spatial part. There are 4 possible spin states for this system:

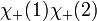
$\chi_+(1)\chi_+(2)$

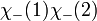
$\chi_-(1)\chi_-(2)$

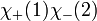
$\chi_+(1)\chi_-(2)$

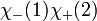
$\chi_-(1)\chi_+(2)$

However, only the first two are symmetric or anti-symmetric to electron exchange (which corresponds to exchanging 1 and 2). The last two need to be rewritten as:

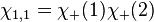
$\chi_{1,1} = \chi_+(1)\chi_+(2)$

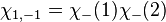
$\chi_{1,-1} = \chi_-(1)\chi_-(2)$

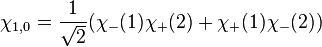
$\chi_{1,0} = \frac{1}{\sqrt{2}} (\chi_-(1)\chi_+(2)+\chi_+(1)\chi_-(2))$

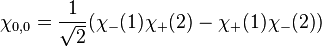
$\chi_{0,0} = \frac{1}{\sqrt{2}} (\chi_-(1)\chi_+(2)-\chi_+(1)\chi_-(2))$

The first three are symmetric, whereas the last one is anti-symmetric. Say one of the electrons in the helium atom is excited to the 2s state. In this case, its spatial wavefunction will have to be either anti-symmetric (requiring a symmetric spin wavefunction):

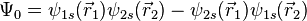
$\Psi_{0} = \psi_{1s} (\vec{r}_1) \psi_{2s} (\vec{r}_2) - \psi_{2s} (\vec{r}_1) \psi_{1s} (\vec{r}_2)$

Or symmetric (requiring an anti-symmetric spin wavefunction):

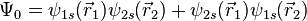
$\Psi_{0} = \psi_{1s} (\vec{r}_1) \psi_{2s} (\vec{r}_2) + \psi_{2s} (\vec{r}_1) \psi_{1s} (\vec{r}_2)$

In the first case, the possible spin states are the three symmetric ones listed above, and this state is commonly referred to as a triplet. The triplet state is not allowed in the ground state of the helium atom, since the spatial function in this case is symmetric and the spin function needs to be anti-symmetric. We can observe that if we take 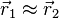$\vec{r}_1 \approx \vec{r}_2$ , the probability amplitude tends to zero, meaning that the electrons are unlikely to be close to each other, which is referred to as Fermi hole and is responsible for the space-occupying properties of matter.

Similarly, in the second case, there is only one possible spin state, 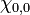$\chi_{0,0}$ , and so this state is commonly referred to as a singlet. We can also observe that the probability amplitude is higher when electrons are close to each other, which means that it is slightly more likely that the electrons will be observed together. This phenomenon is referred to as Fermi heap, and plays an important role in chemical bonding by allowing both electrons to be localized in the internuclear region and thus shielding the positively charged nuclei from electrostatic repulsion with one another.

Since electrons repel one another, Fermi holes and Fermi heaps have drastic effects on the energy of many-electron atoms, such as the periodic properties of the elements. Since bringing electrons together requires doing work, Fermi heaps have higher energy than Fermi holes. This result is generalized in terms of multiplicity by Hund's rule which states that the higher the spin multiplicity of a state (number of spin states it is allowed to have by the exclusion principle), the lower its energy will be.

Animations of Fermi holes and Fermi heaps in the carbon atom are here.^[1] Details of the origin and significance of Fermi holes and Fermi heaps in the structure of atoms are discussed here.^[2]

References

↑ Dill, Dan, Fermi holes and Fermi heaps. URL checked 18 June 2009
↑ Dill, Dan, Many-electron atoms: Fermi holes and Fermi heaps. URL checked 18 June 2009

Dill, Dan (2006). Notes on General Chemistry (2nd ed.), Chapter 3.5, Many-electron atoms: Fermi holes and Fermi heaps. W. H. Freeman. ISBN 0-393-97661-0.