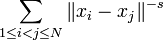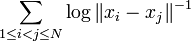Fekete problem
In mathematics, the Fekete problem is, given a natural number N and a real s ≥ 0, to find the points x1,...,xN on the 2-sphere for which the s-energy, defined by
for s > 0 and by
for s = 0, is minimal. For s > 0, such points are called s-Fekete points, and for s = 0, logarithmic Fekete points (see Saff & Kuijlaars (1997)). More generally, one can consider the same problem on the d-dimensional sphere, or on a Riemannian manifold (in which case ||xi −xj|| is replaced with the Riemannian distance between xi and xj).
The problem originated in the paper by Michael Fekete (1923) who considered the one-dimensional, s = 0 case, answering a question of Issai Schur.
An algorithmic version of the Fekete problem is number 7 on the list of problems discussed by Smale (1998).
References
- Bendito, E.; Carmona, A.; Encinas, A. M.; Gesto, J. M.; Gómez, A.; Mouriño, C.; Sánchez, M. T. (2009), "Computational cost of the Fekete problem. I. The forces method on the 2-sphere", Journal of Computational Physics 228 (9): 3288–3306, doi:10.1016/j.jcp.2009.01.021, ISSN 0021-9991, MR 2513833
- Fekete, M. (1923), "Über die Verteilung der Wurzeln bei gewissen algebraischen Gleichungen mit ganzzahligen Koeffizienten", Mathematische Zeitschrift 17 (1): 228–249, doi:10.1007/BF01504345, ISSN 0025-5874, MR 1544613
- Saff, E. B.; Kuijlaars, A. B. J. (1997). "Distributing many points on a sphere". Math. Intelligencer 19 (1): 5–11. doi:10.1007/BF03024331. MR 1439152.
- Smale, Stephen (1998), "Mathematical problems for the next century", The Mathematical Intelligencer 20 (2): 7–15, doi:10.1007/BF03025291, ISSN 0343-6993, MR 1631413