Fay's trisecant identity

In algebraic geometry, Fay's trisecant identity is an identity between theta functions of Riemann surfaces introduced by Fay (1973, chapter 3, page 34, formula 45). Fay's identity holds for theta functions of Jacobians of curves, but not for theta functions of general abelian varieties.

The name "trisecant identity" refers to the geometric interpretation given by Mumford (1984, p.3.219), who used it to show that the Kummer variety of a genus g Riemann surface, given by the image of the map from the Jacobian to projective space of dimension 2^g – 1 induced by theta functions of order 2, has a 4-dimensional space of trisecants.

Statement

Suppose that

C is a compact Riemann surface
g is the genus of C
θ is the Riemann theta function of C, a function from C^g to C
E is a prime form on C×C
u,v,x,y are points of C
z is an element of C^g
ω is a 1-form on C with values in C^g

The Fay's identity states that

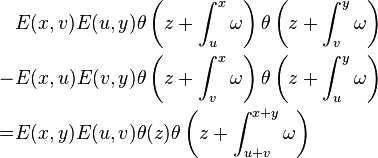
$\begin{align} &E(x,v)E(u,y)\theta\left(z+\int_u^x\omega\right)\theta\left(z+\int_v^y\omega\right)\\ - &E(x,u)E(v,y)\theta\left(z+\int_v^x\omega\right)\theta\left(z+\int_u^y\omega\right)\\ = &E(x,y)E(u,v)\theta(z)\theta\left(z+\int_{u+v}^{x+y}\omega\right) \end{align}$

with

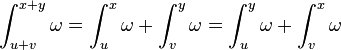
$\begin{align} &\int_{u+v}^{x+y}\omega=\int_u^x\omega+\int_v^y\omega=\int_u^y\omega+\int_v^x\omega \end{align}$

References

Fay, John D. (1973), Theta functions on Riemann surfaces, Lecture Notes in Mathematics 352, Berlin, New York: Springer-Verlag, doi:10.1007/BFb0060090, ISBN 978-3-540-06517-3, MR 0335789
Mumford, David (1974), "Prym varieties. I", in Ahlfors, Lars V.; Kra, Irwin; Nirenberg, Louis et al., Contributions to analysis (a collection of papers dedicated to Lipman Bers), Boston, MA: Academic Press, pp. 325–350, ISBN 978-0-12-044850-0, MR 0379510 |displayeditors= suggested (help)
Mumford, David (1984), Tata lectures on theta. II, Progress in Mathematics 43, Boston, MA: Birkhäuser Boston, ISBN 978-0-8176-3110-9, MR 742776