Faxén's law
In fluid dynamics, Faxén's laws relate a sphere's velocity 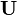 and angular velocity
and angular velocity 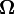 to the forces, torque, stresslet and flow it experiences under low Reynolds number (creeping flow) conditions.
to the forces, torque, stresslet and flow it experiences under low Reynolds number (creeping flow) conditions.
First law
Faxen's first law was introduced in 1922 by Swedish physicist Hilding Faxén, who at the time was active at Uppsala University, and is given by[1][2]
where
-
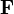 is the force exerted by the fluid on the sphere
is the force exerted by the fluid on the sphere -
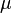 is the Newtonian viscosity of the solvent in which the sphere is placed
is the Newtonian viscosity of the solvent in which the sphere is placed -
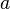 is the sphere's radius
is the sphere's radius -
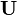 is the (translational) velocity of the sphere
is the (translational) velocity of the sphere -
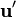 is the disturbance velocity caused by the other spheres in suspension (not by the background impressed flow), evaluated at the sphere centre
is the disturbance velocity caused by the other spheres in suspension (not by the background impressed flow), evaluated at the sphere centre -
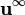 is the background impressed flow, evaluated at the sphere centre (set to zero in some references).
is the background impressed flow, evaluated at the sphere centre (set to zero in some references).
It can also be written in the form
where 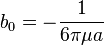 is the mobility.
is the mobility.
In the case that the pressure gradient is small compared with the length scale of the sphere's diameter, and when there is no external force, the last two terms of this form may be neglected. In this case the external fluid flow simply advects the sphere.
Second law
Faxen's second law is given by[1][2]
where
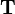 is the torque exerted by the fluid on the sphere
is the torque exerted by the fluid on the sphere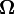 is the angular velocity of the sphere
is the angular velocity of the sphere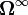 is the angular velocity of the background flow, evaluated at the sphere centre (set to zero in some references).
is the angular velocity of the background flow, evaluated at the sphere centre (set to zero in some references).
'Third law'
Batchelor and Green[3] derived an equation for the stresslet, given by[1][2]
where
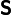 is the stresslet (symmetric part of the first moment of force) exerted by the fluid on the sphere,
is the stresslet (symmetric part of the first moment of force) exerted by the fluid on the sphere,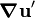 is the velocity gradient tensor;
is the velocity gradient tensor; 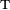 represents transpose; and so
represents transpose; and so ![\frac{1}{2}\left[\boldsymbol{\nabla} \mathbf{u}' + (\boldsymbol{\nabla} \mathbf{u}')^\mathrm{T}\right]](../I/m/1023b607da78a3f7798a3a04cac1ac8f.png) is the rate of strain, or deformation, tensor.
is the rate of strain, or deformation, tensor.![\boldsymbol{\mathsf{E}}^\infty = \frac{1}{2}\left[\boldsymbol{\nabla} \mathbf{u}^\infty + (\boldsymbol{\nabla} \mathbf{u}^\infty)^\mathrm{T}\right]](../I/m/b0dd331bfca65936cb863451b84f081f.png) is the rate of strain of the background flow, evaluated at the sphere centre (set to zero in some references).
is the rate of strain of the background flow, evaluated at the sphere centre (set to zero in some references).
Note there is no rate of strain on the sphere (no 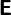 ) since the spheres are assumed to be rigid.
) since the spheres are assumed to be rigid.
Faxén's law is a correction to Stokes' law for the friction on spherical objects in a viscous fluid, valid where the object moves close to a wall of the container.[4]
See also
Notes
- ↑ 1.0 1.1 1.2 Chen, Shing Bor; Ye, Xiangnan (2000). "Faxen's laws of a composite sphere under creeping flow conditions". Journal of colloid and interface science 221 (1): 50–57. doi:10.1006/jcis.1999.6552.
- ↑ 2.0 2.1 2.2 Durlofsky, Louis, John F. Brady, and Georges Bossis. "Dynamic simulation of hydrodynamically interacting particles." Journal of fluid mechanics 180.1 (1987): 21-49 doi:10.1017/S002211208700171X, equations (2.15a, b, c). Note sign change.
- ↑ http://dx.doi.org/10.1017/S0022112072002435 Batchelor, G. K., and J. T. Green. "The hydrodynamic interaction of two small freely-moving spheres in a linear flow field." J. Fluid Mech 56.2 (1972): 375-400
- ↑ Single molecule measurements and biological motors - Glossary, accessed on May 12, 2009
References
- Faxén, H. (1922), "Der Widerstand gegen die Bewegung einer starren Kugel in einer zähen Flüssigkeit, die zwischen zwei parallelen ebenen Wänden eingeschlossen ist", Annalen der Physik 373 (10): 89–119, Bibcode:1922AnP...373...89F, doi:10.1002/andp.19223731003
- Happel, J.; Brenner, H. (1991), Low Reynolds Number Hydrodynamics, Dordrecht: Kluwer
![\mathbf{F} = 6 \pi \mu a \left[ \left( 1 + \frac{a^2}{6} \nabla^2\right) \mathbf{u}' - (\mathbf{U} - \mathbf{u}^\infty) \right],](../I/m/c05cfc1978ce1c2a9f45f6a76dc726af.png)
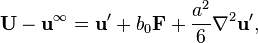
![\mathbf{T} = 8 \pi \mu a^3 \left[ \frac{1}{2} \left( \boldsymbol{\nabla} \times \mathbf{u}' \right) - (\mathbf{\Omega} - \mathbf{\Omega}^\infty) \right],](../I/m/f169e0c532d208bc578ee59109b3d572.png)
![\boldsymbol{\mathsf{S}} = \frac{10}{3} \pi \mu a^3 \left[ -2\boldsymbol{\mathsf{E}}^\infty + \left(1 + \frac{1}{10} a^2 \nabla^2\right) \left(\boldsymbol{\nabla} \mathbf{u}' + (\boldsymbol{\nabla} \mathbf{u}')^\mathrm{T}\right)\right],](../I/m/38268ca21d56e8ac8f184601b7940610.png)