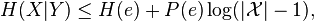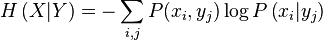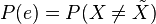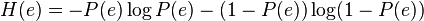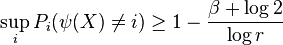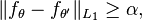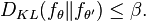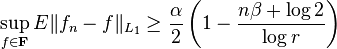Fano's inequality
In information theory, Fano's inequality (also known as the Fano converse and the Fano lemma) relates the average information lost in a noisy channel to the probability of the categorization error. It was derived by Robert Fano in the early 1950s while teaching a Ph.D. seminar in information theory at MIT, and later recorded in his 1961 textbook.
It is used to find a lower bound on the error probability of any decoder as well as the lower bounds for minimax risks in density estimation.
Let the random variables X and Y represent input and output messages with a joint probability 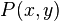 . Let e represent an occurrence of error; i.e., that
. Let e represent an occurrence of error; i.e., that 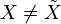 , being
, being 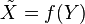 a noise approximate version of
a noise approximate version of  . Fano's inequality is
. Fano's inequality is
where 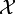 denotes the support of X,
denotes the support of X,
is the conditional entropy,
is the probability of the communication error, and
is the corresponding binary entropy.
Alternative formulation
Let X be a random variable with density equal to one of 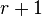 possible densities
possible densities 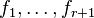 . Furthermore, the Kullback–Leibler divergence between any pair of densities cannot be too large,
. Furthermore, the Kullback–Leibler divergence between any pair of densities cannot be too large,
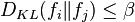 for all
for all 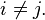
Let 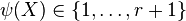 be an estimate of the index. Then
be an estimate of the index. Then
where 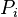 is the probability induced by
is the probability induced by 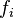
Generalization
The following generalization is due to Ibragimov and Khasminskii (1979), Assouad and Birge (1983).
Let F be a class of densities with a subclass of r + 1 densities ƒθ such that for any θ ≠ θ′
Then in the worst case the expected value of error of estimation is bound from below,
where ƒn is any density estimator based on a sample of size n.
References
- P. Assouad, "Deux remarques sur l'estimation", Comptes Rendus de L'Academie des Sciences de Paris, Vol. 296, pp. 1021–1024, 1983.
- L. Birge, "Estimating a density under order restrictions: nonasymptotic minimax risk", Technical report, UER de Sciences Économiques, Universite Paris X, Nanterre, France, 1983.
- T. Cover, J. Thomas, Elements of Information Theory. pp. 43.
- L. Devroye, A Course in Density Estimation. Progress in probability and statistics, Vol 14. Boston, Birkhauser, 1987. ISBN 0-8176-3365-0, ISBN 3-7643-3365-0.
- R. Fano, Transmission of information; a statistical theory of communications. Cambridge, Massachusetts, M.I.T. Press, 1961. ISBN 0-262-06001-9
- R. Fano, Fano inequality Scholarpedia, 2008.
- I. A. Ibragimov, R. Z. Has′minskii, Statistical estimation, asymptotic theory. Applications of Mathematics, vol. 16, Springer-Verlag, New York, 1981. ISBN 0-387-90523-5