Factorial moment generating function
In probability theory and statistics, the factorial moment generating function of the probability distribution of a real-valued random variable X is defined as
for all complex numbers t for which this expected value exists. This is the case at least for all t on the unit circle 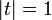 , see characteristic function. If X is a discrete random variable taking values only in the set {0,1, ...} of non-negative integers, then
, see characteristic function. If X is a discrete random variable taking values only in the set {0,1, ...} of non-negative integers, then 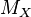 is also called probability-generating function of X and
is also called probability-generating function of X and 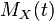 is well-defined at least for all t on the closed unit disk
is well-defined at least for all t on the closed unit disk 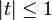 .
.
The factorial moment generating function generates the factorial moments of the probability distribution.
Provided 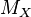 exists in a neighbourhood of t = 1, the nth factorial moment is given by [1]
exists in a neighbourhood of t = 1, the nth factorial moment is given by [1]
where the Pochhammer symbol (x)n is the falling factorial
(Many mathematicians, especially in the field of special functions, use the same notation to represent the rising factorial.)
Example
Suppose X has a Poisson distribution with expected value λ, then its factorial moment generating function is
(use the definition of the exponential function) and thus we have
See also
- Moment (mathematics)
- Moment-generating function
- Cumulant-generating function
![M_X(t)=\operatorname{E}\bigl[t^{X}\bigr]](../I/m/97b2aa9bc0946fe385455f9cb3af5f25.png)
![\operatorname{E}[(X)_n]=M_X^{(n)}(1)=\left.\frac{\mathrm{d}^n}{\mathrm{d}t^n}\right|_{t=1} M_X(t),](../I/m/6f5e4f5505d9b570f207521ff6e0e4be.png)
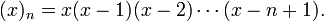
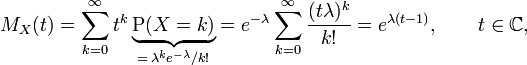
![\operatorname{E}[(X)_n]=\lambda^n.](../I/m/8fed9fea74c5c112d8f27d152dc98856.png)