Face configuration
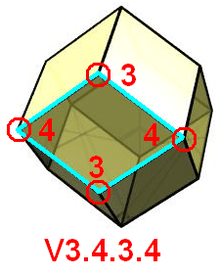
V3.4.3.4
In geometry, a face configuration is notational description of a face-transitive polyhedron. It represents a sequential count of the number of faces that exist at each vertex around a face.
It is called a Cundy-Rollett symbol with a period seperators, like the vertex configuration, but with a V prefix for the uniform dual Catalan solids in their 1952 book Mathematical Models. There is no single standard accepted representation, and others separate terms by a comma (,). Another form of this notation, used in Tilings and Patterns, has brackets around the symbol for planar tilings, for instance [3.6.3.6] for a trihexagonal tiling.
For example, V3.4.3.4 represents the rhombic dodecahedron which is face-transitive: every face is a rhombus, and alternating vertices of the rhombus contain 3 or 4 faces each.
Face-transitive polyhedra are generally the polyhedral duals of the vertex-transitive polyhedra, which are described by a parallel vertex configuration notation. That notation omits the V prefix and represents sequentially the number of edges of the faces around a vertex. For example, 3.4.3.4 is the cuboctahedron with alternating triangular and square faces around each vertex. Polyhedra have the same representation in face configuration notation (with the addition of the V) that their duals have in vertex configuration notation. The rhombic dodecahedron (V3.4.3.4) and the cubocahedron (3.4.3.4) above are dual polyhedra.
See also
- Platonic solids: five regular polyhedra that are either self-dual or whose dual is another Platonic solid.
- Catalan solids: thirteen polyhedra that are dual to the Archimedean solids
- Bipyramids: an infinite set of duals of prisms
- Trapezohedra: an infinite set of duals of antiprisms
- List of uniform planar tilings
References
- Cundy, H. and Rollett, A., Mathematical Models (1952), (3rd edition, 1989, Stradbroke, England: Tarquin Pub.) P.118-119 Table I, Nets of Archimedean Duals
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. Uses Cundy-Rollett symbol
- Branko Grünbaum and G. C. Shephard Tilings and Patterns. New York: W. H. Freeman & Co., 1987. ISBN 0-7167-1193-1.