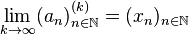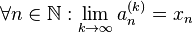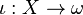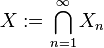FK-space
In functional analysis and related areas of mathematics a FK-space or Fréchet coordinate space is a sequence space equipped with a topological structure such that it becomes a Fréchet space. FK-spaces with a normable topology are called BK-spaces.
There exists only one topology to turn a sequence space into a Fréchet space, namely the topology of pointwise convergence. Thus the name coordinate space because a sequence in an FK-space converges if and only if it converges for each coordinate.
FK-spaces are examples of topological vector spaces. They are important in summability theory.
Definition
A FK-space is a sequence space  , that is a linear subspace of vector space of all complex valued sequences, equipped with the topology of pointwise convergence.
, that is a linear subspace of vector space of all complex valued sequences, equipped with the topology of pointwise convergence.
We write the elements of  as
as
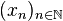 with
with 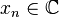
Then sequence 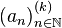 in
in  converges to some point
converges to some point 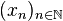 if it converges pointwise for each
if it converges pointwise for each  . That is
. That is
if
Examples
- The sequence space
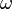 of all complex valued sequences is trivially an FK-space.
of all complex valued sequences is trivially an FK-space.
Properties
Given an FK-space  and
and 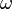 with the topology of pointwise convergence the inclusion map
with the topology of pointwise convergence the inclusion map
is continuous.
FK-space constructions
Given a countable family of FK-spaces 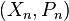 with
with  a countable family of semi-norms, we define
a countable family of semi-norms, we define
and
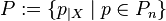 .
.
Then 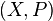 is again an FK-space.
is again an FK-space.
See also
- BK-space, FK-spaces with a normable topology