F-term
In theoretical physics, one often analyzes theories with supersymmetry in which F-terms play an important role. In four dimensions, the minimal N=1 supersymmetry may be written using a superspace. This superspace involves four extra fermionic coordinates 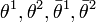 , transforming as a two-component spinor and its conjugate.
, transforming as a two-component spinor and its conjugate.
Every superfield—i.e. a field that depends on all coordinates of the superspace—may be expanded with respect to the new fermionic coordinates. There exists a special kind of superfields, the so-called chiral superfields, that only depend on the variables  but not their conjugates. The last term in the corresponding expansion, namely
but not their conjugates. The last term in the corresponding expansion, namely 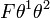 , is called the F-term. Applying an infinitesimal supersymmetry transformation to a chiral superfield results in yet another chiral superfield whose F-term, in particular, changes by a total derivative. This is significant because then
, is called the F-term. Applying an infinitesimal supersymmetry transformation to a chiral superfield results in yet another chiral superfield whose F-term, in particular, changes by a total derivative. This is significant because then 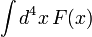 is invariant under SUSY transformations as long as boundary terms vanish. Thus F-terms may be used in constructing supersymmetric actions.
is invariant under SUSY transformations as long as boundary terms vanish. Thus F-terms may be used in constructing supersymmetric actions.
Manifestly-supersymmetric Lagrangians may also be written as integrals over the whole superspace. Some special terms, such as the superpotential, may be written as integrals over  s only. They are also referred to as F-terms, much like the terms in the ordinary potential that arise from these terms of the supersymmetric Lagrangian.
s only. They are also referred to as F-terms, much like the terms in the ordinary potential that arise from these terms of the supersymmetric Lagrangian.