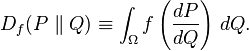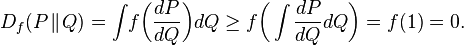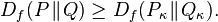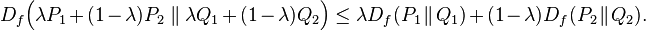f-divergence
In probability theory, an ƒ-divergence is a function Df (P || Q) that measures the difference between two probability distributions P and Q. It helps the intuition to think of the divergence as an average, weighted by the function f, of the odds ratio given by P and Q.
These divergences were introduced and studied independently by Csiszár (1963), Morimoto (1963) and Ali & Silvey (1966) and are sometimes known as Csiszár ƒ-divergences, Csiszár-Morimoto divergences or Ali-Silvey distances.
Definition
Let P and Q be two probability distributions over a space Ω such that P is absolutely continuous with respect to Q. Then, for a convex function f such that f(1) = 0, the f-divergence of Q from P is defined as
If P and Q are both absolutely continuous with respect to a reference distribution μ on Ω then their probability densities p and q satisfy dP = p dμ and dQ = q dμ. In this case the f-divergence can be written as
The f-divergences can be expressed using Taylor series and rewritten using a weighted sum of chi-type distances (Nielsen & Nock (2013)).
Instances of f-divergences
Many common divergences, such as KL-divergence, Hellinger distance, and total variation distance, are special cases of f-divergence, coinciding with a particular choice of f. The following table lists many of the common divergences between probability distributions and the f function to which they correspond (cf. Liese & Vajda (2006)).
| Divergence | Corresponding f(t) |
|---|---|
| KL-divergence | 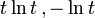 |
| Hellinger distance | 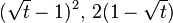 |
| Total variation distance |  |
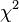 -divergence -divergence |
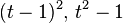 |
| α-divergence | 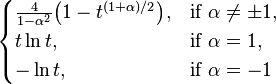 |
Properties
- Non-negativity: the ƒ-divergence is always positive; it's zero if and only if the measures P and Q coincide. This follows immediately from Jensen’s inequality:
-
- Monotonicity: if κ is an arbitrary transition probability that transforms measures P and Q into Pκ and Qκ correspondingly, then
-
- Joint Convexity: for any 0 ≤ λ ≤ 1
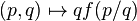 on
on  .
. -
References
- Csiszár, I. (1963). "Eine informationstheoretische Ungleichung und ihre Anwendung auf den Beweis der Ergodizitat von Markoffschen Ketten". Magyar. Tud. Akad. Mat. Kutato Int. Kozl 8: 85–108.
- Morimoto, T. (1963). "Markov processes and the H-theorem". J. Phys. Soc. Jap. 18 (3): 328–331. doi:10.1143/JPSJ.18.328.
- Ali, S. M.; Silvey, S. D. (1966). "A general class of coefficients of divergence of one distribution from another". Journal of the Royal Statistical Society, Series B 28 (1): 131–142. JSTOR 2984279. MR 0196777.
- Csiszár, I. (1967). "Information-type measures of difference of probability distributions and indirect observation". Studia Scientiarum Mathematicarum Hungarica 2: 229–318.
- Csiszár, I.; Shields, P. (2004). "Information Theory and Statistics: A Tutorial" (PDF). Foundations and Trends in Communications and Information Theory 1 (4): 417–528. doi:10.1561/0100000004. Retrieved 2009-04-08.
- Liese, F.; Vajda, I. (2006). "On divergences and informations in statistics and information theory". IEEE Transactions on Information Theory 52 (10): 4394–4412. doi:10.1109/TIT.2006.881731.
- Nielsen, F.; Nock, R. (2013). "On the Chi square and higher-order Chi distances for approximating f-divergences". arXiv. 1309.3029.
- Coeurjolly, J-F.; Drouihet, R. (2006). "Normalized information-based divergences". arXiv:math/0604246.