Exposed point

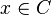In mathematics, an exposed point of a convex set $C$ is a point $x\in C$ at which some continuous linear functional attains its strict maximum over $C$ . Such a functional is then said to expose $x$ . Note that there can be many exposing functionals for $x$ . The set of exposed points of $C$ is usually denoted $\exp(C)$ .

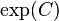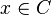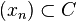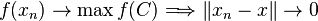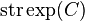A stronger notion is that of strongly exposed point of $C$ which is an exposed point $x \in C$ such that some exposing functional $f$ of $x$ attains its strong maximum over $C$ at $x$ , i.e. for each sequence $(x_n) \subset C$ we have the following implication: $f(x_n) \to \max f(C) \Longrightarrow \|x_n -x\| \to 0$ . The set of all strongly exposed points of $C$ is usually denoted $\operatorname{str}\exp(C)$ .

There are two weaker notions, that of extreme point and that of support point of $C$ .