Exponentially equivalent measures
In mathematics, exponential equivalence of measures is how two sequences or families of probability measures are “the same” from the point of view of large deviations theory.
Definition
Let (M, d) be a metric space and consider two one-parameter families of probability measures on M, say (με)ε>0 and (νε)ε>0. These two families are said to be exponentially equivalent if there exist
- a one-parameter family of probability spaces ((Ω, Σε, Pε))ε>0,
- two families of M-valued random variables (Yε)ε>0 and (Zε)ε>0,
such that
- for each ε > 0, the Pε-law (i.e. the push-forward measure) of Yε is με, and the Pε-law of Zε is νε,
- for each δ > 0, “Yε and Zε are further than δ apart” is a Σε-measurable event, i.e.
- for each δ > 0,
The two families of random variables (Yε)ε>0 and (Zε)ε>0 are also said to be exponentially equivalent.
Properties
The main use of exponential equivalence is that as far as large deviations principles are concerned, exponentially equivalent families of measures are indistinguishable. More precisely, if a large deviations principle holds for (με)ε>0 with good rate function I, and (με)ε>0 and (νε)ε>0 are exponentially equivalent, then the same large deviations principle holds for (νε)ε>0 with the same good rate function I.
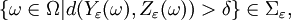
![\limsup_{\varepsilon \downarrow 0} \varepsilon \log \mathbf{P}_{\varepsilon} \big[ d(Y_{\varepsilon}, Z_{\varepsilon}) > \delta \big] = - \infty.](../I/m/c6bc960858af555fa7233af497df85b0.png)