Exponential dispersion model

Exponential dispersion models are statistical models in which the probability distribution is of a special form.^[1]^[2] This class of models represents a generalisation of the exponential family of models which themselves play an important role in statistical theory because they have a special structure which enables deductions to be made about appropriate statistical inference.

Definition

Exponential dispersion models are a generalisation of the natural exponential family: these have a probability density function which, for a multivariate model, can be written as

f_X(\mathbf{x}|\boldsymbol{\theta}) = h(\mathbf{x}) \exp(\boldsymbol\theta^\top \mathbf{x} - A(\boldsymbol\theta)) \,\! ,

where the parameter 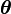$\boldsymbol\theta$ has the same dimension as the observation variable 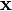$\mathbf{x}$ . The generalisation includes an extra scalar "index parameter", 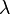$\lambda$ , and has density function of the form^[2]

f_X(\mathbf{x}|\lambda,\boldsymbol{\theta}) = h(\lambda,\mathbf{x}) \exp (\lambda [\boldsymbol\theta^\top \mathbf{x} - A(\boldsymbol\theta)] ) \,\! .

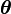The terminology "dispersion parameter" is used for $\sigma^2=\lambda^{-1}$ , while $\boldsymbol\theta$ is the "natural parameter" (also known as "canonical parameter").

References

↑ Marriott, P. (2005) "Local Mixtures and Exponential Dispersion Models" pdf
↑ 2.0 2.1 Jørgensen, B. (1987). Exponential dispersion models (with discussion). Journal of the Royal Statistical Society, Series B, 49 (2), 127–162.