Explicit reciprocity law
In mathematics, an explicit reciprocity law is a formula for the Hilbert symbol of a local field. The name "explicit reciprocity law" refers to the fact that the Hilbert symbols of local fields appear in Hilbert's reciprocity law for the power residue symbol. The definitions of the Hilbert symbol are usually rather roundabout and can be hard to use directly in explicit examples, and the explicit reciprocity laws give more explicit expressions for the Hilbert symbol that are sometimes easier to use.
There are also several explicit reciprocity laws for various generalizations of the Hilbert symbol to higher local fields, p-divisible groups, and so on.
History
Artin & Hasse (1928) gave an explicit formula for the Hilbert symbol (α,β) in the case of odd prime powers, for some special values of α and β when the field is the (cyclotomic) extension of the p-adic numbers by a pnth root of unity. Iwasawa (1968) extended the formula of Artin and Hasse to more cases of α and β, and Wiles (1978) and de Shalit (1986) extended Iwasawa's work to Lubin–Tate extensions of local fields. Shafarevich (1950) gave an explicit formula for the Hilbert symbol for odd prime powers for general local fields. His formula was rather complicated which made it hard to use, and Brückner (1967, 1979) and Vostokov (1978) found a simpler formula. Henniart (1981) simplified Vostokov's work and extended it to the case of even prime powers.
Examples
For archimedean local fields or in the unramified case the Hilbert symbol is easy to write down explicitly. The main problem is to evaluate it in the ramified case.
Archimedean fields
Over the complex numbers (a, b) is always 1. Over the reals, the Hilbert symbol of odd degree is trivial, and the Hilbert symbol of even degree is given by (a, b)∞ is +1 if at least one of a or b is positive, and −1 if both are negative.
Unramified case: the tame Hilbert symbol
In the unramified case, when the order of the Hilbert symbol is coprime to the residue characteristic of the local field, the tame Hilbert symbol is given by[1]
where ω(a) is the (q – 1)-th root of unity congruent to a and ord(a) is the value of the valuation of the local field, and n is the degree of the Hilbert symbol, and q is the order of the residue class field. The number n divides q – 1 because the local field contains the nth roots of unity by assumption.
As a special case, over the p-adics with p odd, writing  and
and  , where u and v are integers coprime to p, we have for the quadratic Hilbert symbol
, where u and v are integers coprime to p, we have for the quadratic Hilbert symbol
 , where
, where 
and the expression involves two Legendre symbols.
Ramified case
The simplest example of a Hilbert symbol in the ramified case is the quadratic Hilbert symbol over the 2-adic integers.
Over the 2-adics, again writing  and
and  , where u and v are odd numbers, we have for the quadratic Hilbert symbol
, where u and v are odd numbers, we have for the quadratic Hilbert symbol
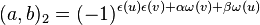 , where
, where 
See also
Notes
- ↑ Neukirch (1999) p.335
References
- Artin, E.; Hasse, H. (1928), "Die beiden Ergänzungssätze zum Reziprozitätsgesetz der ln-ten Potenzreste im Körper der ln-ten Einheitswurzeln", Abhandlungen Hamburg 6: 146–162, doi:10.1007/bf02940607, JFM 54.0191.05
- Brückner, Helmut (1967), "Eine explizite Formel zum Reziprozitätsgesetz für Primzahlexponenten p", Algebraische Zahlentheorie (Ber. Tagung Math. Forschungsinst. Oberwolfach, 1964) (in German), Bibliographisches Institut, Mannheim, pp. 31–39, MR 0230702
- Brückner, H. (1979), Explizites Reziprozitätsgesetz und Anwendungen, Vorlesungen aus dem Fachbereich Mathematik der Universität Essen (in German) 2, Universität Essen, Fachbereich Mathematik, Essen, MR 0533354
- de Shalit, Ehud (1986), "The explicit reciprocity law in local class field theory", Duke Math. J. 53 (1): 163–176, doi:10.1215/s0012-7094-86-05311-1, MR 0835803
- Henniart, Guy (1981), "Sur les lois de réciprocité explicites. I.", J. Reine Angew. Math. (in French) 329: 177–203, MR 0636453
- Iwasawa, Kenkichi (1968), "On explicit formulas for the norm residue symbol", J. Math. Soc. Japan 20: 151–165, doi:10.2969/jmsj/02010151, MR 0229609
- Neukirch, Jürgen (1999), Algebraic Number Theory, Grundlehren der mathematischen Wissenschaften 322, Berlin: Springer-Verlag, ISBN 978-3-540-65399-8, Zbl 0956.11021, MR 1697859
- Shafarevich, I. R. (1950), "A general reciprocity law", Mat. Sbornik N.S. (in Russian) 26: 113–146, MR 0031944
- Vostokov, S. V. (1978), "An explicit form of the reciprocity law", Izv. Akad. Nauk SSSR Ser. Mat. 42 (6): 1288–1321, 1439, doi:10.1070/IM1979v013n03ABEH002077, MR 0522940
- Wiles, A. (1978), "Higher explicit reciprocity laws", Annals of Mathematics 107 (2): 235–254, doi:10.2307/1971143, MR 0480442
Further reading
- Lemmermeyer, Franz (2000), Reciprocity laws. From Euler to Eisenstein, Springer Monographs in Mathematics, Berlin: Springer-Verlag, ISBN 3-540-66957-4, MR 1761696, Zbl 0949.11002
