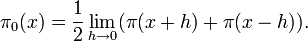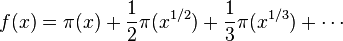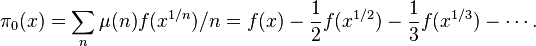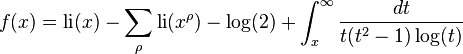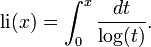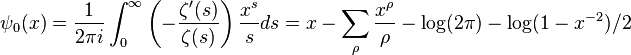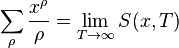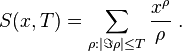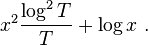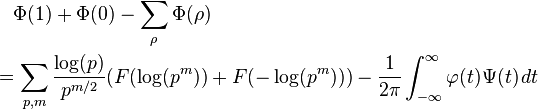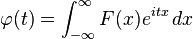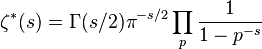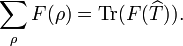Explicit formulae (L-function)

In mathematics, the explicit formulae for L-functions are relations between sums over the complex number zeroes of an L-function and sums over prime powers, introduced by Riemann (1859) for the Riemann zeta function. Such explicit formulae have been applied also to questions on bounding the discriminant of an algebraic number field, and the conductor of a number field.

Riemann's explicit formula

In his 1859 paper On the Number of Primes Less Than a Given Magnitude Riemann found an explicit formula for the normalized prime-counting function π₀(x) which is related to the prime-counting function π(x) by

\pi_0(x) = \frac{1}{2} \lim_{h\to 0} (\pi(x+h) + \pi(x-h)).

His formula was given in terms of the related function

f(x) =\pi(x)+\frac{1}{2}\pi(x^{1/2})+\frac{1}{3}\pi(x^{1/3})+\cdots

which counts primes where a prime power pⁿ counts as 1/n of a prime and which takes the arithmetic mean of the limit from the left and the limit from the right at discontinuities. The normalized prime-counting function can be recovered from this function by

\pi_0(x) = \sum_n\mu(n)f(x^{1/n})/n = f(x) -\frac{1}{2}f(x^{1/2})-\frac{1}{3}f(x^{1/3}) - \cdots.

Riemann's formula is then

f(x) = \operatorname{li}(x) - \sum_\rho \operatorname{li}(x^\rho) -\log(2) +\int_x^\infty\frac{dt}{t(t^2-1)\log(t)}

involving a sum over the non-trivial zeros ρ of the Riemann zeta function. The sum is not absolutely convergent, but may be evaluated by taking the zeros in order of the absolute value of their imaginary part. The function li occurring in the first term is the (unoffset) logarithmic integral function given by the Cauchy principal value of the divergent integral

\operatorname{li}(x) = \int_0^x\frac{dt}{\log(t)}.

The terms li(x^ρ) involving the zeros of the zeta function need some care in their definition as li has branch points at 0 and 1, and are defined by analytic continuation in the complex variable ρ in the region x>1 and Re(ρ)>0. The other terms also correspond to zeros: the dominant term li(x) comes from the pole at s = 1, considered as a zero of multiplicity −1, and the remaining small terms come from the trivial zeros. This formula says that the zeros of the Riemann zeta function control the oscillations of primes around their "expected" positions. (For graphs of the sums of the first few terms of this series see Zagier 1977.)

A simpler variation of Riemann's formula using the normalization 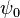$\psi_0$ of Chebyshev's function ψ rather than π is^[1] von-Mangoldt's explicit formula

\psi_0(x) = \dfrac{1}{2\pi i}\int_0^{\infty}\left(-\dfrac{\zeta'(s)}{\zeta(s)}\right)\dfrac{x^s}{s}ds=x-\sum_\rho\frac{x^\rho}{\rho} - \log(2\pi) -\log(1-x^{-2})/2

where for non-integral x, ψ(x) is the sum of log(p) over all prime powers pⁿ less than x. It plays an important role in von Mangoldt's proof of Riemann's explicit formula.

Here the sum over zeroes should again be taken in increasing order of imaginary part:^[2]

\sum_\rho\frac{x^\rho}{\rho} = \lim_{T \rightarrow \infty} S(x,T) \

where

S(x,T) = \sum_{\rho:|\Im \rho| \le T} \frac{x^\rho}{\rho} \ .

The error involved in truncating the sum to S(x,T) is of order^[2]

x^2 \frac{\log^2 T}{T} + \log x \ .

Weil's explicit formula

There are several slightly different ways to state the explicit formula. Weil's form of the explicit formula states

\begin{align} & {} \quad \Phi(1)+\Phi(0)-\sum_\rho\Phi(\rho) \\ & = \sum_{p,m} \frac{\log(p)}{p^{m/2}} (F(\log(p^m)) + F(-\log(p^m))) - \frac{1}{2\pi} \int_{-\infty}^\infty\varphi(t)\Psi(t)\,dt \end{align}

where

ρ runs over the non-trivial zeros of the zeta function
p runs over positive primes
m runs over positive integers
F is a smooth function all of whose derivatives are rapidly decreasing
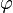$\varphi$ is a Fourier transform of F:

\varphi(t) = \int_{-\infty}^\infty F(x)e^{itx}\,dx

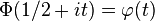
$\Phi(1/2 + it) = \varphi(t)$
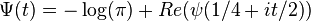$\Psi(t) = - \log( \pi ) + Re(\psi(1/4 + it/2))$ , where 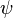$\psi$ is the digamma function Γ′/Γ.

Roughly speaking, the explicit formula says the Fourier transform of the zeros of the zeta function is the set of prime powers plus some elementary factors.

The terms in the formula arise in the following way.

The terms on the right hand side come from the logarithmic derivative of

\zeta^*(s)= \Gamma(s/2)\pi^{-s/2}\prod_p \frac{1}{1-p^{-s}}

with the terms corresponding to the prime p coming from the Euler factor of p, and the term at the end involving Ψ coming from the gamma factor (the Euler factor at infinity).

The left-hand side is a sum over all zeros of ζ^* counted with multiplicities, so the poles at 0 and 1 are counted as zeros of order −1.

Generalizations

The Riemann zeta function can be replaced by a Dirichlet L-function of a Dirichlet character χ. The sum over prime powers then gets extra factors of χ(p^m), and the terms Φ(1) and Φ(0) disappear because the L-series has no poles.

More generally, the Riemann zeta function and the L-series can be replaced by the Dedekind zeta function of an algebraic number field or a Hecke L-series. The sum over primes then gets replaced by a sum over prime ideals.

Applications

Riemann's original use of the explicit formula was to give an exact formula for the number of primes less than a given number. To do this, take F(log(y)) to be y^1/2/log(y) for 0 ≤ y ≤ x and 0 elsewhere. Then the main term of the sum on the right is the number of primes less than x. The main term on the left is Φ(1); which turns out to be the dominant terms of the prime number theorem, and the main correction is the sum over non-trivial zeros of the zeta function. (There is a minor technical problem in using this case, in that the function F does not satisfy the smoothness condition.)

Hilbert–Pólya conjecture

According to the Hilbert–Pólya conjecture, the complex zeroes ρ should be the eigenvalues of some linear operator T. The sum over the zeros of the explicit formula is then (at least formally) given by a trace:

\sum_\rho F(\rho) = \operatorname{Tr}(F(\widehat T )).\!

Development of the explicit formulae for a wide class of L-functions was given by Weil (1952), who first extended the idea to local zeta-functions, and formulated a version of a generalized Riemann hypothesis in this setting, as a positivity statement for a generalized function on a topological group. More recent work by Alain Connes has gone much further into the functional-analytic background, providing a trace formula the validity of which is equivalent to such a generalized Riemann hypothesis. A slightly different point of view was given by Ralf Meyer. Meyer has derived the explicit formula of Weil via harmonic analysis on adelic spaces.

References

↑ Weisstein, Eric W. Explicit Formula on MathWorld.
↑ 2.0 2.1 Ingham (1990) p.77

Ingham, A.E. (1990) [1932], The Distribution of Prime Numbers, Cambridge Tracts in Mathematics and Mathematical Physics 30, reissued with a foreword by R. C. Vaughan (2nd ed.), Cambridge University Press, ISBN 978-0-521-39789-6, MR 1074573, Zbl 0715.11045
Lang, Serge (1994), Algebraic number theory, Graduate Texts in Mathematics 110 (2nd ed. ed.), New York, NY: Springer-Verlag, ISBN 0-387-94225-4, Zbl 0811.11001
Riemann, Bernhard (1859), "Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse", Monatsberichte der Berliner Akademie
Weil, André (1952), "Sur les "formules explicites" de la théorie des nombres premiers", Comm. Sém. Math. Univ. Lund [Medd. Lunds Univ. Mat. Sem.] Suppl.-band M. Riesz (in French) 1952: 252–265, MR 0053152, Zbl 0049.03205
Mangoldt, Hans von (1895), "Zu Riemanns Abhandlung "Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse"", Journal für die reine und angewandte Mathematik (in German) 114: 255–305, ISSN 0075-4102, Zbl 26.0215.03
Meyer, Ralf (2005), "On a representation of the idele class group related to primes and zeros of L-functions", Duke Math. Journal 127 (3): 519–595, doi:10.1215/s0012-7094-04-12734-4, ISSN 0012-7094, Zbl 1079.11044
Montgomery, Hugh L.; Vaughan, Robert C. (2007), Multiplicative number theory. I. Classical theory, Cambridge Studies in Advanced Mathematics 97, Cambridge: Cambridge University Press, ISBN 0-521-84903-9, Zbl 1142.11001
Patterson, S.J. (1988), An introduction to the theory of the Riemann zeta-function, Cambridge Studies in Advanced Mathematics 14, Cambridge: Cambridge University Press, ISBN 0-521-33535-3, Zbl 0641.10029