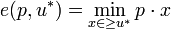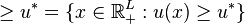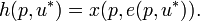Expenditure minimization problem
In microeconomics, the expenditure minimization problem is another perspective on the utility maximization problem: "how much money do I need to reach a certain level of happiness?". This question comes in two parts. Given a consumer's utility function, prices, and a utility target,
- how much money would the consumer need? This is answered by the expenditure function.
- what could the consumer buy to meet this utility target while minimizing expenditure? This is answered by the Hicksian demand function.
Expenditure function
Formally, the expenditure function is defined as follows. Suppose the consumer has a utility function  defined on
defined on  commodities. Then the consumer's expenditure function gives the amount of money required to buy a package of commodities at given prices
commodities. Then the consumer's expenditure function gives the amount of money required to buy a package of commodities at given prices  that give utility of at least
that give utility of at least 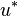 ,
,
where
is the set of all packages that give utility at least as good as 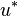 .
.
Hicksian demand correspondence
Secondly, the Hicksian demand function 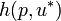 is defined as the cheapest package that gives the desired utility. It can be defined in terms of the expenditure function with the Marshallian demand function
is defined as the cheapest package that gives the desired utility. It can be defined in terms of the expenditure function with the Marshallian demand function
The relationship between the utility function and Marshallian demand in the utility maximization problem mirrors the relationship between the expenditure function and Hicksian demand in the expenditure minimization problem. It is also possible that the Hicksian and Marshallian demands are not unique (i.e. there is more than one commodity bundle that satisfies the expenditure minimization problem); then the demand is a correspondence, and not a function. This does not happen, and the demands are functions, under the assumption of local nonsatiation.
See also
References
- Mas-Colell, Andreu; Whinston, Michael & Green, Jerry (1995). Microeconomic Theory. Oxford: Oxford University Press. ISBN 0-19-507340-1.