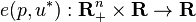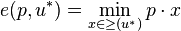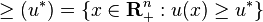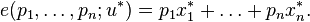Expenditure function
In microeconomics, the expenditure function gives the minimum amount of money an individual needs to spend to achieve some level of utility, given a utility function and the prices of the available goods.
Formally, if there is a utility function 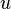 that describes preferences over n commodities, the expenditure function
that describes preferences over n commodities, the expenditure function
says what amount of money is needed to achieve a utility 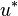 if the n prices are given by the price vector
if the n prices are given by the price vector 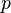 .
This function is defined by
.
This function is defined by
where
is the set of all bundles that give utility at least as good as 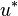 .
.
Expressed equivalently, the individual minimizes expenditure 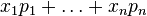 subject to the minimal utility constraint that
subject to the minimal utility constraint that 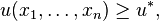 giving optimal quantities to consume of the various goods as
giving optimal quantities to consume of the various goods as 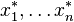 as functions of
as functions of 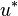 and the prices; then the expenditure function is
and the prices; then the expenditure function is
See also
- Expenditure minimization problem
- Hicksian demand function
- Slutsky equation
- Utility maximization problem
References
- Mas-Colell, Andreu; Whinston, Michael D.; Green, Jerry R. (2007). Microeconomic Theory. pp. 59–60. ISBN 0-19-510268-1.
- Mathis, Stephen A.; Koscianski, Janet (2002). Microeconomic Theory: An Integrated Approach. Upper Saddle River: Prentice Hall. pp. 132–133. ISBN 0-13-011418-9.
- Varian, Hal R. (1984). Microeconomic Analysis (Second ed.). New York: W. W. Norton. pp. 121–123. ISBN 0-393-95282-7.