Expansion path

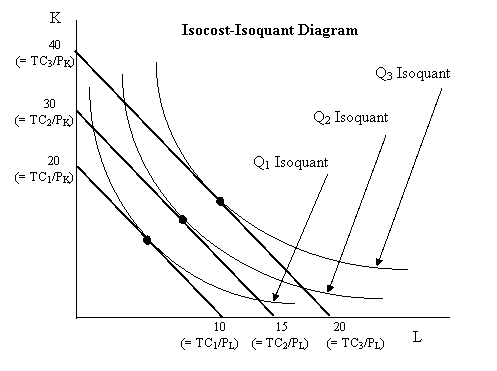
Isocost v. Isoquant Graph. Each line segment is an isocost line representing one particular level of total input costs, denoted TC, with PL being the unit price of labor and PK the unit price of physical capital. The convex curves are isoquants, each showing various combinations of input usages that would give the particular output level designated by the particular isoquant. Tangency points show the lowest cost input combination for producing any given level of output. A curve connecting the tangency points is called the expansion path because it shows how the input usages expand as the chosen level of output expands.

In economics, an expansion path (also called a scale line[1]) is a curve in a graph with quantities of two inputs, typically capital and labor, plotted on the axes. The path connects optimal input combinations as the scale of production expands.[2] A producer seeking to produce the most units of a product in the cheapest possible way attempts to increase production along the expansion path.[3]

Economists Alfred Stonier and Douglas Hague defined expansion path as "that line which reflects the least cost method of producing different levels of output, when factor prices remain constant."[4] The points on an expansion path occur where the firm's isocost curves, each showing fixed total input cost, and its isoquants, each showing a particular level of output, are tangent. As a producer's allowable total cost increases, the firm moves from one of these tangency points to the next; the line joining the tangency points is called the expansion path.[5]

If an expansion path forms a straight line from the origin, the production technology is considered homothetic (or homoethetic).[6] In this case, the ratio of input usages is always the same regardless of the level of output, and the inputs can be expanded proportionately so as to maintain this optimal ratio as the allowable total cost expands. A Cobb–Douglas production function is an example of a production function that has an expansion path which is a straight line through the origin.[6]

See also

References

  1. ↑ Jain, TR; Khanna OP (2008). Economics. VK Publications, ISBN 978-81-87344-77-3
  2. ↑ Hirschey, Mark (2008). Managerial economics. Cengage Learning, ISBN 978-0-324-58886-6
  3. ↑ Prusty, Sadananda (2010). Managerial Economics. PHI Learning Pvt. Ltd., ISBN 978-81-203-4094-7
  4. ↑ Stonier, Alfred W.; Hague, Douglas C. (1980). A textbook of economic theory, 5th edition. Longmans ISBN 978-0-582-29530-8
  5. ↑ Salvatore, Dominick (1989). Schaum's outline of theory and problems of managerial economics. McGraw-Hill, ISBN 978-0-07-054513-7
  6. ↑ 6.0 6.1 Rasmussen, Svend (2011). Production Economics: The Basic Theory of Production Optimisation. Springer, ISBN 978-3-642-14609-1

External links