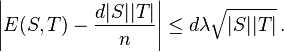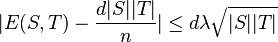Expander mixing lemma

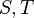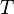The expander mixing lemma states that, for any two subsets $S, T$ of a d-regular expander graph $G$ with $n$ vertices, the number of edges between $S$ and $T$ is approximately what you would expect in a random d-regular graph, i.e. $d|S| |T| / n$ .

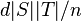Statement

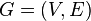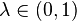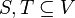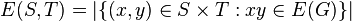Let $G = (V, E)$ be a d-regular graph on n vertices with $\lambda\in(0,1)$ the second-largest eigenvalue (in absolute value) of the normalized adjacency matrix. For any two subsets $S, T \subseteq V$ , let $E(S, T) = |\{(x,y) \in S \times T : xy \in E(G)\}|$ be the number of edges between S and T (counting edges contained in the intersection of S and T twice). Then

\left|E(S, T) - \frac{d |S| |T|}{n}\right| \leq d \lambda \sqrt{|S| |T|}\,.

Proof

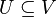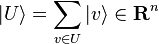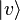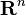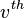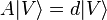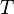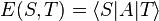Let $A$ be the adjacency matrix for $G$ . For a vertex subset $U \subseteq V$ , let $|U\rangle = \sum_{v \in U} |v\rangle \in \mathbf{R}^n$ . Here $|v\rangle$ is the standard basis element of $\mathbf{R}^n$ with a one in the $v^{th}$ position. Thus in particular $A |V\rangle = d |V\rangle$ , and the number of edges between $S$ and $T$ is given by $E(S, T) = \langle S | A | T \rangle$ .

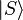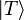Expand each of $|S\rangle$ and $|T\rangle$ into a component in the direction of the largest-eigenvalue eigenvector 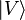$|V\rangle$ and an orthogonal component:

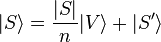
|S\rangle = \frac{|S|}{n} |V\rangle + |S'\rangle

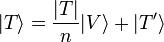|T\rangle = \frac{|T|}{n} |V\rangle + |T'\rangle

where 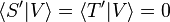$\langle S' | V \rangle = \langle T' | V \rangle = 0$ . Then

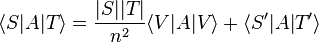\langle S | A | T \rangle = \frac{|S| |T|}{n^2} \langle V | A | V \rangle + \langle S' | A | T' \rangle

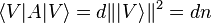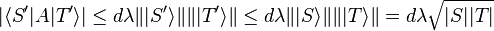The conclusion follows, since $\langle V | A | V \rangle = d \| |V\rangle \|^2 = d n$ , and $| \langle S' | A | T' \rangle | \leq d \lambda \| | S' \rangle \| \| | T' \rangle \| \leq d \lambda \| | S \rangle \| \| | T \rangle \| = d \lambda \sqrt{|S| |T|}$ .

Converse

Bilu and Linial showed that the converse holds as well: if a graph satisfies the conclusion of the expander mixing lemma, that is, for any two subsets 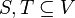$S, T \subseteq V$ ,

|E(S, T) - \frac{d |S| |T|}{n}| \leq d \lambda \sqrt{|S| |T|}

then its second-largest eigenvalue is 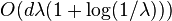$O(d \lambda (1+\log(1/\lambda)))$ .

References

Expander mixing lemma converse.