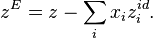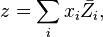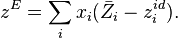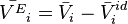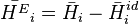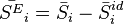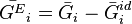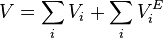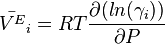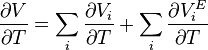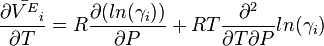Excess molar quantity

Excess molar quantities are properties of mixtures which characterize the nonideal behaviour of real mixtures. They are the difference between the partial molar property of a component in a real mixture and that of the component in an ideal mixture. By definition, excess properties of a mixture are related to those of the pure substances in an ideal mixture by:

z^E=z-\sum_i x_iz^{id}_i.

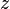Here * denotes the pure substance, E the excess molar property, and z corresponds to the specific property under consideration. From the definition of partial molar properties,

z=\sum_i x_i \bar{Z_i},

substitution yields:

z^E=\sum_i x_i(\bar{Z_i}-z_i^{id}).

For volumes, internal energies and enthalpies the excess quantities are identical to the mixing quantities. They can be expressed as functions of derivatives of the activity coefficients.

Examples

\bar{V^E}_i = \bar V_i - \bar V^{id}_i
\bar{H^E}_i = \bar H_i - \bar H^{id}_i
\bar{S^E}_i = \bar S_i - \bar S^{id}_i
\bar{G^E}_i = \bar G_i - \bar G^{id}_i

The volume of a mixture from the sum of the excess volumes of the components of a mixture is given by the formula:

{V} = \sum_i V_i + \sum_i V_i^{E}

Relation to activity coefficients

The excess molar volume of the component i is connected to its activity coefficient.

\bar{V^E}_i= RT \frac{\partial (ln(\gamma_i))}{\partial P}

Derivatives to state parameters

Thermal expansivities

Deriving by temperature the thermal expansivities of the components in a mixture can be related to the expansivity of the mixture:

\frac{\partial V}{\partial T} = \sum_i \frac{\partial V_i}{\partial T} + \sum_i \frac{\partial V_i^{E}}{\partial T}

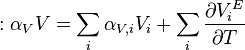
Equivalently: :\alpha_V V = \sum_i \alpha_{V,i} V_i + \sum_i \frac{\partial V_i^{E}}{\partial T}

Substituting the temperature derivative of the excess molar volume

\frac{\partial \bar{V^E}_i}{\partial T} = R \frac{\partial (ln(\gamma_i))}{\partial P} +RT {\partial^2\over\partial T\partial P} ln(\gamma_i)

one can relate activity coefficients to thermal expansivity.

See also

References

Frenkel, Daan; Smit, Berend (2001). Understanding Molecular Simulation : from algorithms to applications. San Diego, California: Academic Press. ISBN 0-12-267351-4.

External links