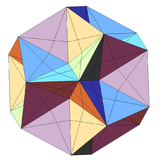
Excavated dodecahedron
| Excavated dodecahedron | |
|---|---|
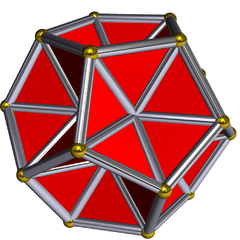 | |
| Type | Stellation |
| Index | W28, 26/59 |
| Elements (As a star polyhedron) | F = 20, E = 60 V = 20 (χ = −20) |
| Faces | 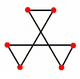 Star hexagon |
| Vertex figure | 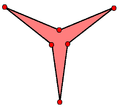 Concave hexagon |
| Symmetry group | icosahedral (Ih) |
| Dual polyhedron | self |

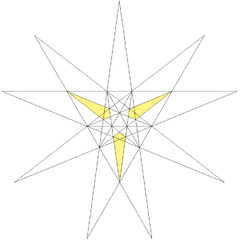
In geometry, the excavated dodecahedron is a star polyhedron having 60 equilateral triangular faces. Its exterior surface represents the Ef1g1 stellation of the icosahedron. It appears in Magnus Wenninger's book Polyhedron Models as model 28, the third stellation of icosahedron.
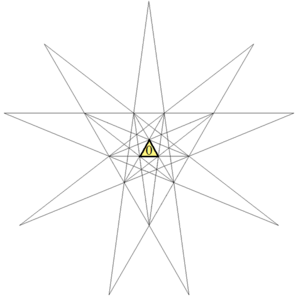
As a stellation
| Stellation diagram | Stellation | Core | Convex hull |
|---|---|---|---|
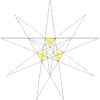 |
 |
 Icosahedron |
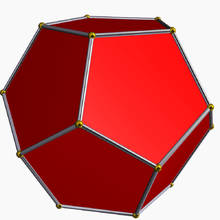 Dodecahedron |
As a faceting
It has the same external form as a certain facetting of the dodecahedron having 20 self-intersecting hexagons as faces. This form is a noble polyhedron.
The 20 vertices of the convex hull match the vertex arrangement of the dodecahedron.
-
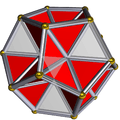
One of the star hexagon faces highlighted.
-
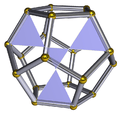
Its face as a facet of the dodecahedron.
The star hexagon face can be broken up into four equilateral triangles, three of which are the same size. A truly excavated dodecahedron would have the three congruent equilateral triangles as true faces of the polyhedron, while the interior equilateral triangle would be fully inside the polyhedron and would thus not be counted.
Related polyhedra
-

It is related to the pentakis dodecahedron, but has inverted pyramids.
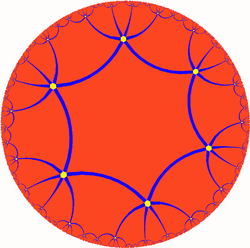
It is topologically equivalent to a quotient space of the hyperbolic order-6 hexagonal tiling and can be topologically deformed into this tiling by making the hexagons regular. As such, it is a regular polyhedron of index two:[1]
References
- ↑ The Regular Polyhedra (of index two), David A. Richter
- H.S.M. Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, 3.6 6.2 Stellating the Platonic solids, pp.96-104
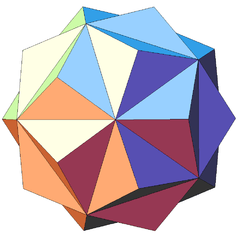
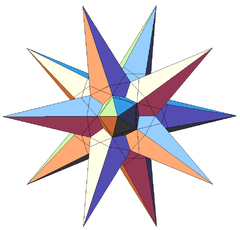
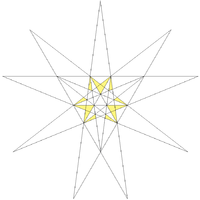
| Notable stellations of the icosahedron | |||||||||
| Regular | Uniform duals | Regular compounds | Regular star | Others | |||||
| (Convex) icosahedron | Small triambic icosahedron | Medial triambic icosahedron | Great triambic icosahedron | Compound of five octahedra | Compound of five tetrahedra | Compound of ten tetrahedra | Great icosahedron | Excavated dodecahedron | Final stellation |
|---|---|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 | |
 |
 |
 |
 |
 |
 |
 |
 |
 | |
| The stellation process on the icosahedron creates a number of related polyhedra and compounds with icosahedral symmetry. | |||||||||